安徽省宿州市十三所重点中学2018-2019学年高一上学期数学期中考试试卷
试卷更新日期:2019-01-03 类型:期中考试
一、单选题
-
1. 集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 下列函数既是增函数,图象又关于原点对称的是( )A、
2. 下列函数既是增函数,图象又关于原点对称的是( )A、 B、
B、 C、
C、 D、
D、 3. 已知 ,则 的大小关系( )A、
3. 已知 ,则 的大小关系( )A、 B、
B、 C、
C、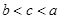 D、
D、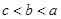 4. 若函数 ,则 的值( )A、2 B、
4. 若函数 ,则 的值( )A、2 B、 C、
C、 D、
5. 函数 在 上是增函数,则 的范围是( )A、
D、
5. 函数 在 上是增函数,则 的范围是( )A、 B、
B、 C、
C、 D、
D、 6. 函数 的零点所在的一个区间是( )A、
6. 函数 的零点所在的一个区间是( )A、 B、
B、 C、
C、 D、
D、 7. 若函数 的定义域为 ,值域为 ,则 的取值范围是( )A、
7. 若函数 的定义域为 ,值域为 ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 8. 已知奇函数 在区间 上是增函数,且最大值为 ,最小值为 ,则在区间 上 的最大值、最小值分别是( )A、
8. 已知奇函数 在区间 上是增函数,且最大值为 ,最小值为 ,则在区间 上 的最大值、最小值分别是( )A、 B、
B、 C、
C、 D、不确定
9. 已知定义在 上的奇函数 的图像关于直线 对称,且 ,则 的值为( )A、
D、不确定
9. 已知定义在 上的奇函数 的图像关于直线 对称,且 ,则 的值为( )A、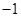 B、
B、 C、
C、 D、2
10. 为了得到函数 的图像,只需把函数 图像上所有的点( )A、向左平移 个单位长度,再向上平移
D、2
10. 为了得到函数 的图像,只需把函数 图像上所有的点( )A、向左平移 个单位长度,再向上平移 个单位长度;
B、向右平移 个单位长度,再向上平移
个单位长度;
B、向右平移 个单位长度,再向上平移  个单位长度;
C、向右平移 个单位长度,再向下平移
个单位长度;
C、向右平移 个单位长度,再向下平移  个单位长度;
D、向左平移 个单位长度,再向下平移
个单位长度;
D、向左平移 个单位长度,再向下平移  个单位长度;
11. 根据有关资料,围棋状态空间复杂度的上限 约为 ,而可观测宇宙中普通物质的原子总数 约为 .则下列各数中与 最接近的是( )(参考数据: )A、
个单位长度;
11. 根据有关资料,围棋状态空间复杂度的上限 约为 ,而可观测宇宙中普通物质的原子总数 约为 .则下列各数中与 最接近的是( )(参考数据: )A、 B、
B、 C、
C、 D、
D、 12. 设函数 ,若互不相等的实数 满足 ,则 的取值范围是( )A、
12. 设函数 ,若互不相等的实数 满足 ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 若幂函数的图象经过点 ,则该函数的解析式为14. 已知函数 的定义域为 ,函数 ,则 的定义域为15. 若 时,恒有 ,则实数 的取值范围是16. 已知函数 ,给出下列结论:
⑴若对任意 ,且 ,都有 ,则 为R上的减函数;
⑵若 为R上的偶函数,且在 内是减函数, (-2)=0,则 >0解集为(-2,2);
⑶若 为R上的奇函数,则 也是R上的奇函数;
⑷t为常数,若对任意的 ,都有 则 关于 对称。
其中所有正确的结论序号为
三、解答题
-
17.(1)、计算(2)、解不等式:18. 已知全集 ,集合 , ,(1)、 ;(2)、若 ,求实数 的取值范围19. 已知 为定义在 上的偶函数,且 时,(1)、求 时,函数 的解析式;(2)、画出函数图象,写出函数 的单调区间(不需证明);(3)、若 恒成立,求 的取值范围
