2016-2017学年江西省萍乡市九年级上学期期末数学试卷
试卷更新日期:2017-04-07 类型:期末考试
一、选择题
-
1. 一元二次方程x2=x的根是( )A、x=1 B、x=0 C、x1=0,x2=1 D、非以上答案2. 当x<0时,反比例函数 的图像( )A、在第二象限内,y随x的增大而减小 B、在第二象限内,y随x的增大而增大 C、在第三象限内,y随x的增大而减小 D、在第三象限内,y随x的增大而增大3. 如图所示,图中几何体的主视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、35. 下列命题正确的是( )A、若两个相似三角形的周长比为3:4,则这两个相似三角形的面积比也是3:4 B、如果两个多边形是相似多边形,那么它们一定是位似图形 C、顺次连接菱形的各边中心所得的四边形是正方形 D、各有一个内角是100°的两个等腰三角形相似6. 将一张矩形纸片ABCD如图所示那样折起,使顶点C落在C′处,其中AB=4,若∠C′ED=30°,则折痕ED的长为( )
4. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、35. 下列命题正确的是( )A、若两个相似三角形的周长比为3:4,则这两个相似三角形的面积比也是3:4 B、如果两个多边形是相似多边形,那么它们一定是位似图形 C、顺次连接菱形的各边中心所得的四边形是正方形 D、各有一个内角是100°的两个等腰三角形相似6. 将一张矩形纸片ABCD如图所示那样折起,使顶点C落在C′处,其中AB=4,若∠C′ED=30°,则折痕ED的长为( )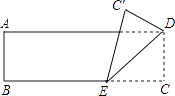 A、4 B、 C、8 D、7. 双曲线y= 与直线y=x没有交点,则k的取值范围是( )A、k<1 B、k>1 C、k<﹣1 D、k>﹣18. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
A、4 B、 C、8 D、7. 双曲线y= 与直线y=x没有交点,则k的取值范围是( )A、k<1 B、k>1 C、k<﹣1 D、k>﹣18. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( ) A、
A、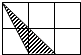 B、
B、 C、
C、 D、
D、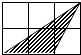 9. 代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:
9. 代数式ax2+bx+c(a≠0,a,b,c是常数)中,x与ax2+bx+c的对应值如下表:x
﹣1
﹣
0
1
2
3
ax2+bx+c
﹣2
﹣
1
2
1
﹣
﹣2
请判断一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1 , x2的取值范围是下列选项中的( )
A、﹣ <x1<0, <x2<2 B、﹣1<x1<﹣ ,2<x2< C、﹣ <x1<0,2<x2< D、﹣1<x1<﹣ , <x2<210. 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )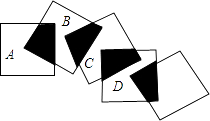 A、2cm2 B、4cm2 C、6cm2 D、8cm2
A、2cm2 B、4cm2 C、6cm2 D、8cm2二、填空题
-
11. 已知一元二次方程x2﹣2x﹣1=0的两个根是x1、x2 , 则x1+x2= , x1x2= , x12+x22= .12. 在△ABC中,D、E分别为AC、BC边上的点,如果 , 那么DE∥AB.(填一个正确的比例式即可)13. 如图,若点A在反比例函数y= (k≠0)的图像上,AM⊥x轴于点M,△AMO的面积为2,则k= .
 14. 均匀的正四面体的各面上依次标有1,2,3,4四个数字,同时抛掷两个这样的正四面体,着地的一面数字之和为5的概率是 .15. 如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是 .
14. 均匀的正四面体的各面上依次标有1,2,3,4四个数字,同时抛掷两个这样的正四面体,着地的一面数字之和为5的概率是 .15. 如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是 .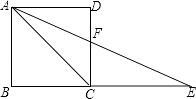 16.
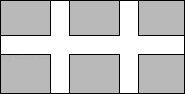
16.如图,某小区有一个长为40米,宽为26米的矩形场地,计划修建一横两纵的三条同样宽度的小路,其余部分种草,若使分割的每一块草坪的面积都为144米2 , 设小路的宽度为x米,则依题意可列方程为 .
 17. 如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数y= 的图像上,则菱形的面积为 .
17. 如图,在平面直角坐标系中,点O为原点,菱形OABC的对角线OB在x轴上,顶点A在反比例函数y= 的图像上,则菱形的面积为 .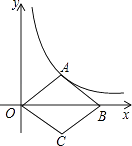 18. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是m.
18. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是m.
三、解答题
-
19. 根据题意解答(1)、用配方法解一元二次方程:x2﹣6x+4=0.(2)、已知关于x的一元二次方程x2﹣4x+m=0的根的判别式的值为4,求m值及方程的根.20. 如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.
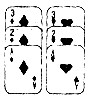 (1)、用列表或树状图的方法表示此游戏所有可能出现的结果;(2)、求摸出的两张牌的牌面数字之和不小于4的概率.21. 如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)、用列表或树状图的方法表示此游戏所有可能出现的结果;(2)、求摸出的两张牌的牌面数字之和不小于4的概率.21. 如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF. (1)、试说明∠BAE=∠DAF;(2)、连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并说明你的理由.22. 随着人民生活水平的不断提高,某市家庭轿车的拥有量逐年增加,据统计,某小区2013年底拥有家庭轿车64辆,2015年底家庭轿车的拥有量达到100辆,若该小区家庭轿车拥有量的年平均增长率相同.(1)、求该小区家庭轿车拥有量的年平均增长率;(2)、该小区到2016年底家庭轿车拥有量将达到多少辆?23. 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:(1)、根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图像,猜测y与x之间的函数关系,并求出该函数关系式:
(1)、试说明∠BAE=∠DAF;(2)、连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并说明你的理由.22. 随着人民生活水平的不断提高,某市家庭轿车的拥有量逐年增加,据统计,某小区2013年底拥有家庭轿车64辆,2015年底家庭轿车的拥有量达到100辆,若该小区家庭轿车拥有量的年平均增长率相同.(1)、求该小区家庭轿车拥有量的年平均增长率;(2)、该小区到2016年底家庭轿车拥有量将达到多少辆?23. 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:(1)、根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图像,猜测y与x之间的函数关系,并求出该函数关系式:x(元)
3
4
5
6
y(个)
20
15
12
10
 (2)、设经营此笔记本的日销售利润为w元,试求出w与x之间的函数关系式;(3)、当日销售单价为8元时,求日销售利润是多少元?24. 如图,教室窗户的高度AF为2.5米,遮阳蓬外端一点D到窗户上椽的距离为AD,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,PE为窗户的一部分在教室地面所形成的影子且长为 米,试求AD的长度.(结果带根号)
(2)、设经营此笔记本的日销售利润为w元,试求出w与x之间的函数关系式;(3)、当日销售单价为8元时,求日销售利润是多少元?24. 如图,教室窗户的高度AF为2.5米,遮阳蓬外端一点D到窗户上椽的距离为AD,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,PE为窗户的一部分在教室地面所形成的影子且长为 米,试求AD的长度.(结果带根号)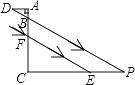 25. 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= ,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.
25. 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= ,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R. (1)、求证:△BFG∽△FEG,并求出BF的长;(2)、求AP:PC的值;(3)、观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程平分)26. 如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E.
(1)、求证:△BFG∽△FEG,并求出BF的长;(2)、求AP:PC的值;(3)、观察图形,请你提出一个与点P相关的问题,并进行解答.(根据提出问题的层次和解答过程平分)26. 如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E. (1)、用含t的代数式分别表示CE和QE的长;(2)、求△APQ的面积s与t的函数表达式;(3)、当QE恰好平分△APQ的面积时,QE的长是多少?
(1)、用含t的代数式分别表示CE和QE的长;(2)、求△APQ的面积s与t的函数表达式;(3)、当QE恰好平分△APQ的面积时,QE的长是多少?