2016-2017学年江西省赣州市章贡区九年级上学期期末数学试卷

试卷更新日期：2017-04-07 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 下列事件中，必然事件是（   ）
    A、打开电视，正在播放新闻 B、抛一枚硬币，正面朝上 C、明天会下雨 D、地球绕着太阳转

    查看试题解析

  • 2. 方程x2﹣3x﹣5=0的根的情况是（　　）

    A、有两个不相等的实数根        B、有两个相等的实数根 C、没有实数根 D、无法确定是否有实数根

    查看试题解析

  • 3. 如图，△ABC为⊙O的内接三角形，AB为⊙O的直径，点D在⊙O上，∠ADC=54°，则∠BAC的度数等于（   ）

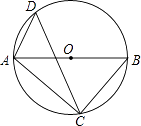    A、36° B、44° C、46° D、54°

    查看试题解析

  • 4. 已知点A（x1 ， y1），B（x2 ， y2）是反比例函数y=﹣ 3x 的图像上的两点，若x1＜0＜x2 ， 则下列结论正确的是（   ）

    A、y1＜0＜y2 B、y2＜0＜y1 C、y1＜y2＜0 D、y2＜y1＜0

    查看试题解析

  • 5. 在平面直角坐标系中，⊙P的圆心坐标为（4，8），半径为5，那么x轴与⊙P的位置关系是（   ）
    A、相交 B、相离 C、相切 D、以上都不是

    查看试题解析

  • 6.

    如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3 ， …组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2015秒时，点P的坐标是（　　）

     

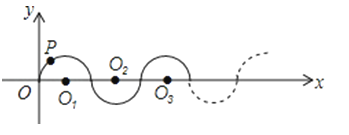    A、（2014，0） B、（2015，﹣1） C、（2015，1） D、（2016，0）

    查看试题解析

二、填空题

  • 7. 将二次函数y=x2的图像向下平移一个单位，则平移以后的二次函数的解析式为 ．

    查看试题解析

  • 8. 在某一时刻，测得一根高为2m的竹竿的影长为1m，同时测得一栋建筑物的影长为12m，那么这栋建筑物的高度为m．

    查看试题解析

  • 9. 已知圆锥的底面半径为1cm，母线长为3cm，则其全面积为cm2 ．

    查看试题解析

  • 10. 如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为 ．

    查看试题解析

  • 11. 已知m，n是方程x2+2x﹣5=0的两个实数根，则m﹣mn+n= ．

    查看试题解析

  • 12. 当﹣2≤x≤1时，二次函数y=﹣（x﹣m）2+m2+1有最大值4，则实数m的范围是 ．

    查看试题解析

三、解答题

  • 13. 根据题意解答
    (1)、解方程：x（x﹣2）+x﹣2=0
    (2)、如图，在已建立直角坐标系的4×4正方形方格纸中，△ABC是格点三角形（三角形的三个顶点都是小正方形的顶点），画出一个以格点P、A、B为顶点的三角形与△ABC相似且不全等．

    查看试题解析

  • 14. 如图，四边形ABCD是⊙O的内接四边形，若∠BOD=88°，求∠BCD的度数．

    查看试题解析

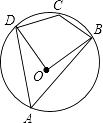  • 15. 抛物线y=2x2平移后经过点A（0，3），B（2，3），求平移后的抛物线的表达式．

    查看试题解析

  • 16. 一个不透明盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，求两次都摸到白球的概率是多少？

    查看试题解析

  • 17. 如图，在△ABC中，∠C=90°，在AB边上取一点D，使BD=BC，过D作DE⊥AB交AC于E，AC=8，BC=6．求DE的长．

    查看试题解析

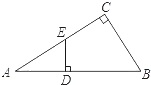  • 18. 如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B，E在反比例函数y= kx 的图像上，OA=1，OC=6，试求出正方形ADEF的边长．

    查看试题解析

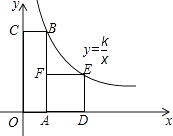  • 19. 如图，E是正方形ABCD中CD边上一点，以点A为中心把△ADE顺时针旋转90°．

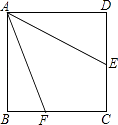    (1)、在图中画出旋转后的图形；
    (2)、若旋转后E点的对应点记为M，点F在BC上，且∠EAF=45°，连接EF．

    ①求证：△AMF≌△AEF；

    ②若正方形的边长为6，AE=3 5 ，求EF．

    查看试题解析

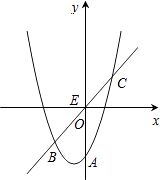
  • 20. 某商店将成本为每件60元的某商品标价100元出售．
    (1)、为了促销，该商品经过两次降低后每件售价为81元，若两次降价的百分率相同，求每次降价的百分率；
    (2)、经调查，该商品每降价2元，每月可多售出10件，若该商品按原标价出售，每月可销售100件，那么当销售价为多少元时，可以使该商品的月利润最大？最大的月利润是多少？

    查看试题解析

  • 21. 如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°．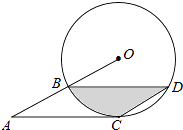

    (1)、求证：AC是⊙O的切线；
    (2)、求图中阴影部分的面积．

    查看试题解析

  • 22. 顶点为（﹣ 12 ，﹣ 174 ）的抛物线与y轴交于点A（0，﹣4），E（0，b）（b＞﹣4）为y轴上一动点，过点E的直线y=x+b与抛物线交于B、C两点．

    (1)、求抛物线的解析式；

    (2)、

    ①如图1，当b=0时，求证：E是线段BC的中点；

    ②当b≠0时，E还是线段BC的中点吗？说明理由．

    查看试题解析

  • 23. 课外兴趣小组活动时，老师提出了如下问题：

    如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．

    小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，再连接BE，（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．

    [感悟]解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．

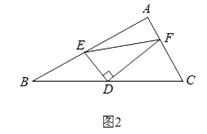
    (1)、解决问题：受到（1）的启发，请你证明下列命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．

    ①求证：BE+CF＞EF；

    ②若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明

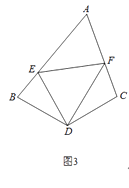
    (2)、问题拓展：如图3，在四边形ABDC中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作一个60°的角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．

    查看试题解析