2016-2017学年河北省唐山市路北区九年级上学期期末数学试卷

试卷更新日期：2017-04-07 类型：期末考试

进入出卷网下载

一、选择题

1. 已知反比例函数y= $\frac{k}{x}$ （k≠0）的图像经过点M（﹣2，2），则k的值是（）

A、﹣4 B、﹣1 C、1 D、4

查看试题解析
2. 在Rt△AABC中，∠C=90°，BC=3，AB=5，则sinA的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

查看试题解析
3. 反比例函数y=﹣ $\frac{1}{x}$ 的图像在（）

A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限

查看试题解析
4. 如果两个相似三角形的相似比是1：2，那么这两个相似三角形的周长比是（）

A、2：1 B、 $1 ： \sqrt{2}$ C、1：4 D、1：2

查看试题解析
5. 在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为（）

A、8m B、10m C、15m D、20m

查看试题解析
6. 如图，⊙O的直径AB=2，点C在⊙O上，弦AC=1，则∠D的度数是（）

A、30° B、60° C、45° D、75°

查看试题解析
7. 若点M（﹣3，a），N（4，﹣6）在同一个反比例函数的图象上，则a的值为（）

A、8 B、﹣8 C、﹣7 D、5

查看试题解析
8. 已知二次函数y=x²+x+c的图像与x轴的一个交点为（2，0），则它与x轴的另一个交点坐标是（）

A、（1，0） B、（﹣1，0） C、（2，0） D、（﹣3，0）

查看试题解析
9. 如图，用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5，弧长是6π，那么围成的圆锥的高度是（）

A、 $\sqrt{11}$ B、5 C、4 D、3

查看试题解析
10. 如图，已知矩形ABCD和矩形EFGO在平面直角坐标系中，点B，F的坐标分别为（﹣4，4），（2，1）．若矩形ABCD和矩形EFGO是位似图形，点P（点P在GC上）是位似中心，则点P的坐标为（）

A、（0，3） B、（0，2.5） C、（0，2） D、（0，1.5）

查看试题解析
11. 如图，一次函数y=ax+b和反比例函数y= $\frac{k}{x}$ 的图像相交于A，B两点，使不等式ax+b＞ $\frac{k}{x}$ 成立的自变量x的取值范围是（）

A、x＜﹣1或x＞4 B、x＜﹣1或0＜x＜4 C、﹣1＜x＜4 D、﹣1＜x＜0或x＞4

查看试题解析
12. 抛物线y= $\frac{1}{3}$ x² ， y=﹣3x² ， y=﹣x² ， y=2x²的图像开口最大的是（）

A、y= $\frac{1}{3}$ x² B、y=﹣3x² C、y=﹣x² D、y=2x²

查看试题解析
13. 将一个半径为5的半圆O，如图折叠，使弧AF经过点O，则折痕AF的长度为（）

A、5 B、5 $\sqrt{2}$ C、5 $\sqrt{3}$ D、10 $\sqrt{3}$

查看试题解析
14.
如图，在平行四边形ABCD中，AC=12，BD=8，P是AC上的一个动点，过点P作EF∥BD，与平行四边形的两条边分别交于点E、F．设CP=x，EF=y，则下列图像中，能表示y与x的函数关系的图像大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

15. 已知 $\frac{a}{6}$ = $\frac{b}{5}$ ，则 $\frac{b}{a}$ 的值为．

查看试题解析
16. 二次函数y=3x²﹣6x﹣3图像的对称轴是．

查看试题解析
17. 如图，在△ABC中，AB=5，D、E分别是边AC和AB上的点，且∠ADE=∠B，DE=2，那么AD•BC= ．

查看试题解析
18. 如图是反比例函数y= $\frac{k}{x}$ 在第二象限内的图像，若图中的矩形OABC的面积为2，则k= ．

查看试题解析

三、解答题

19. 计算：2cos30°﹣tan45°﹣ $\sqrt{{(1 - \tan 60^{\circ})}^{2}}$ ．

查看试题解析
20. 解方程：4x²﹣8x+1=0．

查看试题解析
21. 已知：如图，△ABC中，AD⊥BC于D，AD=200，∠B=30°，∠C=45°．求BC的长．

查看试题解析
22. 如图，在△ABC中，∠C=90°，在AB边上取一点D，使BD=BC，过D作DE⊥AB交AC于E，AC=8，BC=6．求DE的长．

查看试题解析
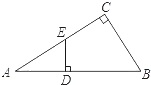23. 如图，直线y=x﹣1与反比例函数y= $\frac{k}{x}$ 的图像交于A、B两点，与x轴交于点C，已知点A的坐标为（﹣1，m）．

(1)、求反比例函数的解析式；

(2)、若点P（n，﹣1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．

查看试题解析
24. 如图，△ABC的边AB为⊙O的直径，BC与⊙O交于点D，D为BC的中点，过点D作DE⊥AC于E．

(1)、求证：AB=AC；

(2)、求证：DE是⊙O的切线；

(3)、若AB=13，BC=10，求CE的长．

查看试题解析
25. 为测量某特种车辆的性能，研究制定了行驶指数P，P=K+1000，而K的大小与平均速度v（km/h）和行驶路程s（km）有关（不考虑其他因素），K由两部分的和组成，一部分与v²成正比，另一部分与sv成正比．在实验中得到了表格中的数据：
速度v
40
60
路程s
40
70
指数P
1000
1600

(1)、用含v和s的式子表示P；

(2)、当行驶指数为500，而行驶路程为40时，求平均速度的值；

(3)、当行驶路程为180时，若行驶指数值最大，求平均速度的值．

查看试题解析
26.
如图，甲、乙两人分别从A（1， $\sqrt{3}$ ），B（6，0）两点同时出发，点O为坐标原点，甲沿AO方向，乙沿BO方向均以4km/h的速度行驶，th后，甲到达M点，乙到达N点．

(1)、请说明甲、乙两人到达O点前，MN与AB不可能平行；

(2)、当t为何值时，△OMN∽△OBA；

(3)、甲、乙两人之间的距离为MN的长，设s=MN² ，直接写出s与t之间的函数关系式．

查看试题解析

速度v	40	60
路程s	40	70
指数P	1000	1600