2016-2017学年广西北海市九年级上学期期末数学试卷
试卷更新日期：2017-04-07 类型：期末考试
一、选择题
-
1. 下列图形是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列事件中，是必然事件的是（ ）A、380人中有两个人的生日在同一天 B、两条线段可以组成一个三角形 C、打开电视机，它正在播放新闻联播 D、三角形的内角和等于360°3. 把方程x2﹣6x+4=0的左边配成完全平方，正确的变形是（ ）A、（x﹣3）2=9 B、（x﹣3）2=13 C、（x+3）2=5 D、（x﹣3）2=54. ⊙O的半径为6cm，点A到圆心O的距离为5cm，那么点A与⊙O的位置关系是（ ）A、点A在圆内 B、点A在圆上 C、点A在圆外 D、不能确定5.如图，AB是⊙O的直径，点C在⊙O上，若∠B=50°，则∠A的度数为（ ）
A、80° B、60° C、40° D、50°6. 二次函数y=x2的图像向右平移2个单位，得到新的函数图象的表达式是（ ）A、y=x2﹣2 B、y=（x﹣2）2 C、y=x2+2 D、y=（x+2）27. 阿联抛一枚质地均匀的硬币，连续抛3次，硬币均正面朝上落地，如果他再抛第4次，那么硬币正面朝上的概率为（ ）A、 B、 C、 D、18. 关于二次函数y=﹣2x2+3，下列说法中正确的是（ ）A、它的开口方向是向上 B、当x＜﹣1时，y随x的增大而增大 C、它的顶点坐标是（﹣2，3） D、它的对称轴是x=﹣29. 如图，当刻度尺的一边与⊙O相切时，另一边与⊙O的两个交点处的读数如图所示（单位：cm），圆的半径是5，那么刻度尺的宽度为（ ）
A、 cm B、4cm C、3cm D、2cm10. 已知关于x的一元二次方程（m﹣2）x2+x+ =0有两个不等的实数根，则实数m的取值范围为（ ）A、 B、 C、 且m≠2 D、 且m≠211. 篮球比赛中，要求每两队之间都进行一场比赛，总共比赛21场，问有多少个队参加比赛？设有x个队参加比赛，则可列方程为（ ）A、1+x+x2=21 B、x2+2x=21 C、x（x﹣1）=21 D、 x（x﹣1）=2112.如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（﹣2，2 ），则点C的坐标为（ ）
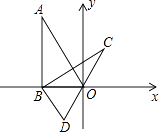A、（ ，1） B、（1， ） C、（1，2） D、（2，1）二、填空题
-
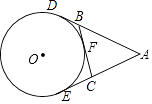
13. 若x=1是一元二次方程x2+2x+m=0的一个根，则m的值为 ．14. 点P（1，﹣2）关于原点的对称点的坐标是 ．15. 一个半径为2cm的圆内接正六边形的面积等于 ．16. 如图，AE，AD，BC分别切⊙O于点E、D和点F，若AD=8cm，则△ABC的周长为cm．
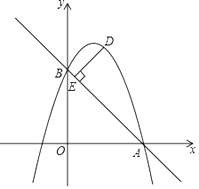
17. 如果圆锥的底面周长为4π cm，侧面展开后所得的扇形的圆心角是120°，则该圆锥的侧面积是cm2 ． （结果保留π）18. 如图，⊙O的半径为2cm，弦BC与弦AD交于点E，且∠CED=75°，弦AB为 cm，则CD的长为cm．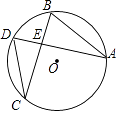
三、解答题
-
19. 解方程：2x2+3x﹣5=0．20.
如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．
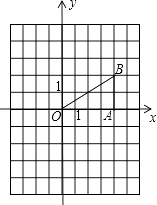(1)、画出将△OAB绕原点旋转180°后所得的△OA1B1 ， 并写出点B1的坐标；(2)、将△OAB平移得到△O2A2B2 ， 点A的对应点是A2（2，﹣4），点B的对应点B2在坐标系中画出△O2A2B2；并写出B2的坐标；(3)、△OA1B1与△O2A2B2成中心对称吗？若是，请直接写出对称中心点P的坐标．21.已知：如图，在正方形ABCD中，F是AB上一点，延长CB到E，使BE=BF，连接CF并延长交AE于G．
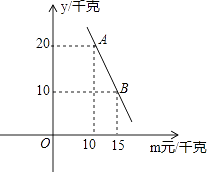
(1)、求证：△ABE≌△CBF；(2)、将△ABE绕点A逆时针旋转90°得到△ADH，请判断四边形AFCH是什么特殊四边形，并说明理由．22. 在北海市创建全国文明城活动中，需要20名志愿者担任“讲文明树新风”公益广告宣传工作，其中男生8人，女生12人．(1)、若从这20人中随机选取一人作为“展板挂图”讲解员，求选到女生的概率；(2)、若“广告策划”只在甲、乙两人中选一人，他们准备以游戏的方式决定由谁担任，游戏规则如下：将四张牌面数字分别为2，3，4，5的扑克牌洗匀后，数字朝下放于桌面，从中任取2张，若牌面数字之和为偶数，则甲担任，否则乙担任．试问这个游戏公平吗？请用树状图或列表法说明理由．23. 我市重庆路水果市场某水果店购进甲、乙两种水果．已知1千克甲种水果的进价比1千克乙种水果的进价多4元，购进2千克甲种水果与1千克乙种水果共需20元．(1)、求甲种水果的进价为每千克多少元？(2)、经市场调查发现，甲种水果每天销售量y（千克）与售价m（元/千克）之间满足如图所示的函数关系，求y与m之间的函数关系；
(3)、在（2）的条件下，当甲种水果的售价定为多少元时，才能使每天销售甲种水果的利润最大？最大利润是多少？24. 我市某高档楼盘准备以每平方米6000元的均价对外销售，由于受市场影响，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．(1)、求平均每次下调的百分率．(2)、某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，另送两年物业管理费，物业管理费每平方米每月1.5元．试问哪种方案更优惠？
