2016-2017学年福建省福州市九年级上学期期末数学试卷
试卷更新日期:2017-04-07 类型:期末考试
一、选择题
-
1. 下列图形中,是中心对称图形的是( )A、
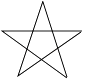 B、
B、 C、
C、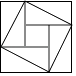 D、
D、 2. 若方程3(x﹣7)(x﹣2)=k的根是7和2,则k的值为( )A、0 B、2 C、7 D、2或73. 气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )A、本市明天将有80%的地区降水 B、本市明天将有80%的时间降水 C、明天肯定下雨 D、明天降水的可能性比较大4. 二次函数y=x2﹣2的顶点坐标是( )A、(0,0) B、(0,﹣2) C、(0,2) D、( ,0)5. 下列图形中,∠B=2∠A的是( )A、
2. 若方程3(x﹣7)(x﹣2)=k的根是7和2,则k的值为( )A、0 B、2 C、7 D、2或73. 气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )A、本市明天将有80%的地区降水 B、本市明天将有80%的时间降水 C、明天肯定下雨 D、明天降水的可能性比较大4. 二次函数y=x2﹣2的顶点坐标是( )A、(0,0) B、(0,﹣2) C、(0,2) D、( ,0)5. 下列图形中,∠B=2∠A的是( )A、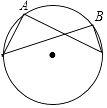 B、
B、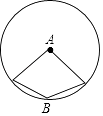 C、
C、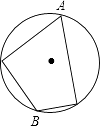 D、
D、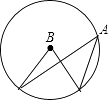 6.
6.在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2 , 那么下列方程符合题意的是( )
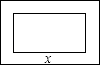 A、(50﹣x)(80﹣x)=5400 B、(50﹣2x)(80﹣2x)=5400 C、(50+x)(80+x)=5400 D、(50+2x)(80+2x)=54007. 正六边形的两条对边之间的距离是2 ,则它的边长是( )A、1 B、2 C、 D、28. 若点M(m,n)(mn≠0)在二次函数y=ax2(a≠0)图像上,则下列坐标表示的点也在该抛物线图像上的是( )A、(﹣m,n) B、(n,m) C、(m2 , n2) D、(m,﹣n)9. 在⊙O中,将圆心绕着圆周上一点A旋转一定角度θ,使旋转后的圆心落在⊙O上,则θ的值可以是( )A、30° B、45° C、60° D、90°10. 圆心角为60°的扇形面积为S,半径为r,则下列图像能大致描述S与r的函数关系的是( )A、
A、(50﹣x)(80﹣x)=5400 B、(50﹣2x)(80﹣2x)=5400 C、(50+x)(80+x)=5400 D、(50+2x)(80+2x)=54007. 正六边形的两条对边之间的距离是2 ,则它的边长是( )A、1 B、2 C、 D、28. 若点M(m,n)(mn≠0)在二次函数y=ax2(a≠0)图像上,则下列坐标表示的点也在该抛物线图像上的是( )A、(﹣m,n) B、(n,m) C、(m2 , n2) D、(m,﹣n)9. 在⊙O中,将圆心绕着圆周上一点A旋转一定角度θ,使旋转后的圆心落在⊙O上,则θ的值可以是( )A、30° B、45° C、60° D、90°10. 圆心角为60°的扇形面积为S,半径为r,则下列图像能大致描述S与r的函数关系的是( )A、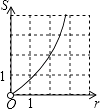 B、
B、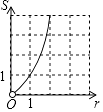 C、
C、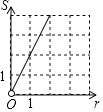 D、
D、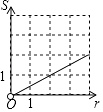
二、填空题
-
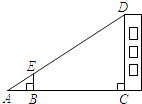
11. 点(0,1)关于原点O对称的点是 .12. 从实数﹣1、﹣2、1中随机选取两个数,积为负数的概率是 .13. 已知∠APB=90°,以AB为直径作⊙O,则点P与⊙O的位置关系是 .14. 如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为 m.
 15. 已知▱ABCD的面积为4,对角线AC在y轴上,点D在第一象限内,且AD∥x轴,当双曲线y= 经过B、D两点时,则k= .16. 二次函数y=(x﹣2m)2+m2 , 当m<x<m+1时,y随x的增大而减小,则m的取值范围是 .
15. 已知▱ABCD的面积为4,对角线AC在y轴上,点D在第一象限内,且AD∥x轴,当双曲线y= 经过B、D两点时,则k= .16. 二次函数y=(x﹣2m)2+m2 , 当m<x<m+1时,y随x的增大而减小,则m的取值范围是 .三、解答题
-
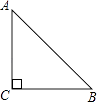
17. 解方程x2+6x+1=0.18. 已知关于x的一元二次方程(x﹣1)2= m﹣1有两个不相等的实数根,求m的取值范围.19. 如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.
 20. 一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.(1)、若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值;(2)、当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.21. 如图,△ABC中,点D在BC边上,有下列三个关系式:
20. 一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.(1)、若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值;(2)、当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.21. 如图,△ABC中,点D在BC边上,有下列三个关系式: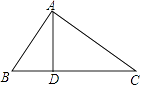
① BAC=90°,② = ,③AD⊥BC.
选择其中两个式子作为已知,余下的一个作为结论,写出已知,求证,并证明.
已知:
求证:
证明:
22. 如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的距离,记录相应的托盘B中的砝码质量,得到下表:
托盘B与点O的距离x(cm)
10
15
20
25
30
托盘B中的砝码质量y(g)
30
20
15
12
10
(1)、把上表中(x,y)的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑曲线连接起来;观察所画的图像,猜测y与x之间的函数关系,求出该函数解析式;(2)、当托盘B向左移动(不超过点M)时,应往托盘B中添加砝码还是减少砝码?23. 如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD= EF=1.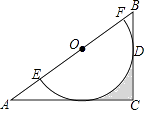 (1)、求证:⊙O与AC相切;(2)、求图中阴影部分的面积.24. 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.(1)、请直接写出点(2,2)的“关联点”的坐标;(2)、如果点P在函数y=x﹣1的图像上,其“关联点”Q与点P重合,求点P的坐标;(3)、如果点M(m,n)的“关联点”N在函数y=x2的图像上,当0≤m≤2时,求线段MN的最大值.25. 如图,C为线段AB上一点,分别以AC、BC为边在AB的同侧作等边△HAC与等边△DCB,连接DH.
(1)、求证:⊙O与AC相切;(2)、求图中阴影部分的面积.24. 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.(1)、请直接写出点(2,2)的“关联点”的坐标;(2)、如果点P在函数y=x﹣1的图像上,其“关联点”Q与点P重合,求点P的坐标;(3)、如果点M(m,n)的“关联点”N在函数y=x2的图像上,当0≤m≤2时,求线段MN的最大值.25. 如图,C为线段AB上一点,分别以AC、BC为边在AB的同侧作等边△HAC与等边△DCB,连接DH.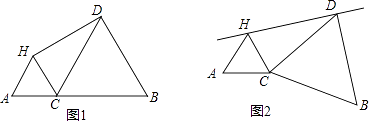 (1)、如图1,当∠DHC=90°时,求 的值;(2)、在(1)的条件下,作点C关于直线DH的对称点E,连接AE、BE,求证:CE平分∠AEB;(3)、现将图1中△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,点C关于直线DH的对称点为E,则(2)中的结论是否成立并证明.
(1)、如图1,当∠DHC=90°时,求 的值;(2)、在(1)的条件下,作点C关于直线DH的对称点E,连接AE、BE,求证:CE平分∠AEB;(3)、现将图1中△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,点C关于直线DH的对称点为E,则(2)中的结论是否成立并证明.