2016-2017学年湖北省鄂州市梁子湖区八年级上学期期末数学试卷
试卷更新日期:2017-04-07 类型:期末考试
一、选择题
-
1. 下列计划图形,不一定是轴对称图形的是( )A、角 B、等腰三角形 C、长方形 D、直角三角形2. 若分式 有意义,则x满足的条件是( )A、x=1 B、x=﹣1 C、x≠1 D、x≠﹣13. 下列运算中正确的是( )A、a3+a3=2a6 B、a2•a3=a6 C、(a2)3=a5 D、a2÷a5=a﹣34. 分式 与 的最简公分母是( )A、ab B、3ab C、3a2b2 D、3a2b65. 如图,点B,F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
 A、BF=EC B、AC=DF C、∠B=∠E D、BF=FC6. 若等腰三角形的两边长分别是4和9,则它的周长是( )A、17 B、22 C、17或22 D、137. 若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为( )A、﹣2 B、2 C、0 D、18. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A、BF=EC B、AC=DF C、∠B=∠E D、BF=FC6. 若等腰三角形的两边长分别是4和9,则它的周长是( )A、17 B、22 C、17或22 D、137. 若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为( )A、﹣2 B、2 C、0 D、18. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )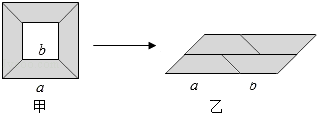 A、a2﹣b2=(a﹣b)2 B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣b2=(a+b)(a﹣b)9. 三角形中,三个内角的比为1:3:6,它的三个外角的比为( )A、1:3:6 B、6:3:1 C、9:7:4 D、3:5:210. 如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )
A、a2﹣b2=(a﹣b)2 B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣b2=(a+b)(a﹣b)9. 三角形中,三个内角的比为1:3:6,它的三个外角的比为( )A、1:3:6 B、6:3:1 C、9:7:4 D、3:5:210. 如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( ) A、BM+CN=MN B、BM﹣CN=MN C、CN﹣BM=MN D、BM﹣CN=2MN
A、BM+CN=MN B、BM﹣CN=MN C、CN﹣BM=MN D、BM﹣CN=2MN二、填空题
-
11. 禽流感病毒的形状一般为球形,直径大约为0.000000102m,该直径用科学记数法表示为 m.12. 一个n边形的内角和是1260°,那么n= .13. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度? .
 14. 已知4y2+my+1是完全平方式,则常数m的值是 .15. 若分式方程:3 无解,则k= .16. 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
14. 已知4y2+my+1是完全平方式,则常数m的值是 .15. 若分式方程:3 无解,则k= .16. 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .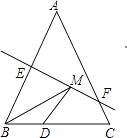
三、解答题
-
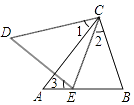
17. 分解因式:(1)、6xy2﹣9x2y﹣y3;(2)、16x4﹣1.18. 先化简,再求值:( + )• ÷( + ),其中x2+y2=17,(x﹣y)2=9.19. 如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.
 20. 如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
20. 如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).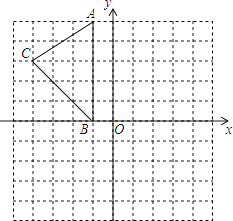 (1)、在图中作出△ABC关于y轴的对称图形△A1B1C1;(2)、在y轴上找出一点P,使得PA+PB的值最小,直接写出点P的坐标;(3)、在平面直角坐标系中,找出一点A2 , 使△A2BC与△ABC关于直线BC对称,直接写出点A2的坐标.21. 甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.(1)、1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?(2)、1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)22. 如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:
(1)、在图中作出△ABC关于y轴的对称图形△A1B1C1;(2)、在y轴上找出一点P,使得PA+PB的值最小,直接写出点P的坐标;(3)、在平面直角坐标系中,找出一点A2 , 使△A2BC与△ABC关于直线BC对称,直接写出点A2的坐标.21. 甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.(1)、1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?(2)、1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)22. 如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证: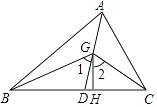 (1)、∠BGC=90°+ ∠BAC;(2)、∠1=∠2.23.
(1)、∠BGC=90°+ ∠BAC;(2)、∠1=∠2.23.如图1,我们在2017年1月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为10×12﹣4×18=48,再选择其他位置的十字星,可以发现“十字差”仍为48.
 (1)、
(1)、如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 .
 (2)、若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.(3)、
(2)、若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.(3)、如图3,将正整数依次填入三角形的数表中,探究不同十字星的“十字差”,若某个十字星中心的数在第32行,且其相应的“十字差”为2017,则这个十字星中心的数为(直接写出结果).
 24. △ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.(1)、如图1,求证:BD=CE;
24. △ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.(1)、如图1,求证:BD=CE;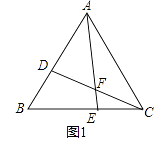 (2)、如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°;
(2)、如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°;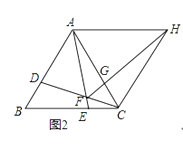 (3)、在(2)的条件下,若AD=2BD,FH=9,求AF长.
(3)、在(2)的条件下,若AD=2BD,FH=9,求AF长.