2016-2017学年广西桂林市八年级上学期期末数学试卷
试卷更新日期:2017-04-07 类型:期末考试
一、选择题
-
1. 下列几个数中,属于无理数的是( )A、 B、2 C、0 D、2. 计算a2•a3的结果是( )A、5a B、a5 C、a6 D、a83. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、4. 25的平方根是( )A、5 B、﹣5 C、± D、±55. 不等式组 的解集在数轴上表示是( )A、
 B、
B、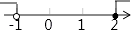 C、
C、 D、
D、 6. 要使式子 有意义,x的取值范围是( )A、x≠1 B、x≠﹣1 C、x≥1 D、x≥﹣17. 下列命题是假命题的是( )A、三角形的内角和是180° B、有一个角是60°的等腰三角形是等边三角形 C、三角形的一个外角等于和它不相邻的两个内角的和 D、平行四边形具有稳定性8. 化简 的结果为( )A、x+y B、x﹣y C、y﹣x D、﹣x﹣y9.
6. 要使式子 有意义,x的取值范围是( )A、x≠1 B、x≠﹣1 C、x≥1 D、x≥﹣17. 下列命题是假命题的是( )A、三角形的内角和是180° B、有一个角是60°的等腰三角形是等边三角形 C、三角形的一个外角等于和它不相邻的两个内角的和 D、平行四边形具有稳定性8. 化简 的结果为( )A、x+y B、x﹣y C、y﹣x D、﹣x﹣y9.如图,△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )
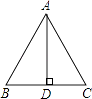 A、△ABD≌△ACD B、∠B=∠C C、AD是∠BAC的平分线 D、△ABC是等边三角形10.
A、△ABD≌△ACD B、∠B=∠C C、AD是∠BAC的平分线 D、△ABC是等边三角形10.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
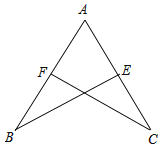 A、2 B、3 C、5 D、2.511. 某班学生军训射击,有m人各打中a环,n人各打中b环,那么该班打中a环和b环学生的平均环数是( )A、 B、 ( + ) C、 D、 (am+bn)12. 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
A、2 B、3 C、5 D、2.511. 某班学生军训射击,有m人各打中a环,n人各打中b环,那么该班打中a环和b环学生的平均环数是( )A、 B、 ( + ) C、 D、 (am+bn)12. 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( ) A、( )5 B、( )5 C、 D、1﹣( )5
A、( )5 B、( )5 C、 D、1﹣( )5二、填空题
-
13. 用科学记数法表示0.000028的结果是 .14. “如果一个数是整数,那么它是有理数”这个命题的条件是 .15. 不等式2+4x>1的解集是 .16.
如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是度.
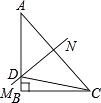 17. 若0≤a≤1,则 = .18. 在△ABC中,AB=AC=9cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的路线运动到C停止.设运动时间为t,过D、P两点的直线将△ABC的周长分成两个部分,若其中一部分是另一部分的2倍,则此时t的值为 .
17. 若0≤a≤1,则 = .18. 在△ABC中,AB=AC=9cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的路线运动到C停止.设运动时间为t,过D、P两点的直线将△ABC的周长分成两个部分,若其中一部分是另一部分的2倍,则此时t的值为 .三、解答题
-
19. 根据题意解答(1)、化简:(﹣x3)2+(2x2)3+(x﹣3)﹣2(2)、计算: ﹣ +( ﹣1)0 .20.
如图,已知线段a,h(a>h),求作等腰三角形ABC,使AB=AC=a,底边BC上的高AD=h(保留作图痕迹,不要求写出作法).
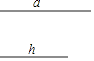 21. 先化简,再求值: ,其中 , .22. 如图,点A,B在数轴上,它们所对应的数分别是﹣3和 ,且点A,B到原点的距离相等,求x的值.
21. 先化简,再求值: ,其中 , .22. 如图,点A,B在数轴上,它们所对应的数分别是﹣3和 ,且点A,B到原点的距离相等,求x的值.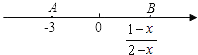 23. 比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴而行,到相距16米的银树下参加探讨环境保护的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后,提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达.已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度.24. 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
23. 比邻而居的蜗牛神和蚂蚁王相约,第二天上午8时结伴而行,到相距16米的银树下参加探讨环境保护的微型动物首脑会议.蜗牛神想到“笨鸟先飞”的古训,于是给蚂蚁王留下一纸便条后,提前2小时独自先行,蚂蚁王按既定时间出发,结果它们同时到达.已知蚂蚁王的速度是蜗牛神的4倍,求它们各自的速度.24. 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.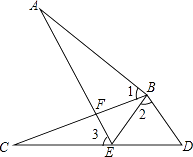 (1)、求证:△ABE≌△CBD;(2)、证明:∠1=∠3.25. 某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)、该班男生和女生各有多少人?(2)、某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?26. 已知等边三角形ABC中,E是AB边上一动点(与A、B不重合),D是CB延长线上的一点,且DE=EC.(1)、当E是AB边上中点时,如图1,线段AE与DB的大小关系是:AEDB(填“>”,“<”或“=”)
(1)、求证:△ABE≌△CBD;(2)、证明:∠1=∠3.25. 某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.(1)、该班男生和女生各有多少人?(2)、某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?26. 已知等边三角形ABC中,E是AB边上一动点(与A、B不重合),D是CB延长线上的一点,且DE=EC.(1)、当E是AB边上中点时,如图1,线段AE与DB的大小关系是:AEDB(填“>”,“<”或“=”)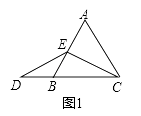 (2)、当E是AB边上任一点时,小敏与同桌小聪讨论后,认为(1)中的结论依然成立,并进行了如下解答:解:如图2,过点E作EF∥BC,交AC于点F
(2)、当E是AB边上任一点时,小敏与同桌小聪讨论后,认为(1)中的结论依然成立,并进行了如下解答:解:如图2,过点E作EF∥BC,交AC于点F(请你按照上述思路,补充完成全部解答过程)
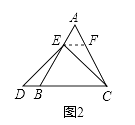 (3)、当E是线段AB延长线上任一点时,如图3.(1)中的结论是否依然成立?若成立,请证明.若不成立,请说明理由.
(3)、当E是线段AB延长线上任一点时,如图3.(1)中的结论是否依然成立?若成立,请证明.若不成立,请说明理由.