2017年四川省广元市高考数学二诊试卷(理科)
试卷更新日期:2017-04-07 类型:高考模拟
一、选择题:
-
1. 若集合A={x|x2+3x﹣4>0},B={x|﹣2<x≤3},且M=A∩B,则有( )A、(∁RB)⊆A B、B⊆A C、2∈M D、1∈M2. 已知z= ﹣ (i是虚数单位).那么复数z的虚部为( )A、 B、i C、1 D、﹣13. 在△ABC中,∠BAC=60°,AB=2,AC=1,E,F为边BC的三等分点,则 =( )A、 B、 C、 D、4. 已知某次数学考试的成绩服从正态分布N(116,82),则成绩在140分以上的考生所占的百分比为( )
(附:正态总体在三个特殊区间内取值的概率值①P(μ﹣σ<X≤μ+σ)=0.6826;②P(μ﹣2σ<X≤μ+2σ)=0.9544;③P(μ﹣3σ<X≤μ+3σ)=0.9974)
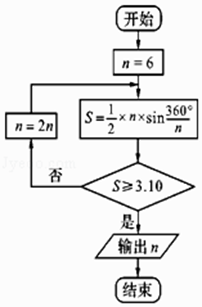
A、0.3% B、0.23% C、1.3% D、0.13%5. 某零件的三视图如图所示,则该零件的体积为( ) A、 B、 C、 D、6. 已知数列{an}的前n项和为Sn , 且对任意正整数n都有an= Sn+2成立.若bn=log2an , 则b1008=( )A、2017 B、2016 C、2015 D、20147. 现用随机模拟方法近似计算积分 dx,先产生两组(每组1000个)在区间[0,2]上的均匀随机数x1 , x2 , x3 , …,x1000和y1 , y2 , y3 , …,y1000 , 由此得到1000个点(xi , yi)(i=1,2,…,1000),再数出其中满足 + ≤1(i=1,2,…,1000)的点数400,那么由随机模拟方法可得积分 dx的近似值为( )A、1.4 B、1.6 C、1.8 D、2.08. 将函数y=2sin(2x+ )的图象向右平移 个单位,所得图象对应的函数( )A、在区间[ , ]上单调递增 B、在区间[ , ]上单调递减 C、在区间[﹣ , ]上单调递增 D、在区间[﹣ , ]上单调递减9. 公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )
A、 B、 C、 D、6. 已知数列{an}的前n项和为Sn , 且对任意正整数n都有an= Sn+2成立.若bn=log2an , 则b1008=( )A、2017 B、2016 C、2015 D、20147. 现用随机模拟方法近似计算积分 dx,先产生两组(每组1000个)在区间[0,2]上的均匀随机数x1 , x2 , x3 , …,x1000和y1 , y2 , y3 , …,y1000 , 由此得到1000个点(xi , yi)(i=1,2,…,1000),再数出其中满足 + ≤1(i=1,2,…,1000)的点数400,那么由随机模拟方法可得积分 dx的近似值为( )A、1.4 B、1.6 C、1.8 D、2.08. 将函数y=2sin(2x+ )的图象向右平移 个单位,所得图象对应的函数( )A、在区间[ , ]上单调递增 B、在区间[ , ]上单调递减 C、在区间[﹣ , ]上单调递增 D、在区间[﹣ , ]上单调递减9. 公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )参考数据: ,sin15°≈0.2588,sin7.5°≈0.1305.
 A、12 B、24 C、48 D、9610. 设等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣2,Sm=0,Sm+1=3,其中m≥2,则nSn的最小值为( )A、﹣3 B、﹣5 C、﹣6 D、﹣911. 已知双曲线C1: 一焦点与抛物线y2=8x的焦点F相同,若抛物线y2=8x的焦点到双曲线C1的渐近线的距离为1,P为双曲线左支上一动点,Q(1,3),则|PF|+|PQ|的最小值为( )A、4 B、4 C、4 D、212. 定义在R上的函数f(x)满足f(x+2)= f(x),当x∈[0,2]时,f(x)= ,函数g(x)=x3+3x2+m.若对任意s∈[﹣4,﹣2),存在t∈[﹣4,﹣2),不等式f(s)﹣g(t)≥0成立,则实数m的取值范围是( )A、(﹣∞,﹣12] B、(﹣∞,14] C、(﹣∞,﹣8] D、(﹣∞, ]
A、12 B、24 C、48 D、9610. 设等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣2,Sm=0,Sm+1=3,其中m≥2,则nSn的最小值为( )A、﹣3 B、﹣5 C、﹣6 D、﹣911. 已知双曲线C1: 一焦点与抛物线y2=8x的焦点F相同,若抛物线y2=8x的焦点到双曲线C1的渐近线的距离为1,P为双曲线左支上一动点,Q(1,3),则|PF|+|PQ|的最小值为( )A、4 B、4 C、4 D、212. 定义在R上的函数f(x)满足f(x+2)= f(x),当x∈[0,2]时,f(x)= ,函数g(x)=x3+3x2+m.若对任意s∈[﹣4,﹣2),存在t∈[﹣4,﹣2),不等式f(s)﹣g(t)≥0成立,则实数m的取值范围是( )A、(﹣∞,﹣12] B、(﹣∞,14] C、(﹣∞,﹣8] D、(﹣∞, ]二、填空题
-
13. 若 + +…+ =256,则 的展开式中含x5项的系数为 . (用数字作答)14. 在条件 ,下,目标函数z=ax+by(a>0,b>0)的最大值为40,则 的最小值是 .15. 如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为 .
 16. 已知函数g(x)=a﹣x2( ≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是 .
16. 已知函数g(x)=a﹣x2( ≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是 .三、解答题:
-
17. 如图,在△ABC中,角A,B,C的对边分别为a,b,c,a=b(sinC+cosC).
(Ⅰ)求∠ABC;
(Ⅱ)若∠A= ,D为△ABC外一点,DB=2,DC=1,求四边形ABDC面积的最大值.
 18. 为了解人们对于国家新颁布的“生育二孩放开”政策的热度,现在对某市年龄在35岁的人调查,随机选取年龄在35岁的100人进行调查,得到他们的情况为:在55名男性中,支持生二孩的有40人,不支持生二孩的有15人;在45名女性中,支持生二孩的有20人,不支持的有25人.
18. 为了解人们对于国家新颁布的“生育二孩放开”政策的热度,现在对某市年龄在35岁的人调查,随机选取年龄在35岁的100人进行调查,得到他们的情况为:在55名男性中,支持生二孩的有40人,不支持生二孩的有15人;在45名女性中,支持生二孩的有20人,不支持的有25人.(Ⅰ)完成下面2×2列联表,并判断有多大的把握认为“支持生二孩与性别有关”?
支持生二孩
不支持生二孩
合计
男性
女性
合计
附:K2= ,其中n=a+b+c+d
P(K2≥k0)
0.150
0.100
0.050
0.010
0.005
0.001
k0
2.072
2.706
3.841
6.635
7.879
10.828
(Ⅱ)在被调查的人员中,按分层抽样的方法从支持生二孩的人中抽取6人,再用简单随机抽样的方法从这6人中随机抽取2人,求这2人中恰好有1名男性的概率;
(Ⅲ)以上述样本数据估计总体,从年龄在35岁人中随机抽取3人,记这3人中支持生二孩且为男性的人数为X,求X的分布列和数学期望.
19. 如图,在四棱锥E﹣ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.(Ⅰ)求证:BE=DE;
(Ⅱ)若AB=2 ,AE=3 ,平面EBD⊥平面ABCD,直线AE与平面ABD所成的角为45°,求二面角B﹣AE﹣D的余弦值.
 20. 已知点P是椭圆C上任一点,点P到直线l1:x=﹣2的距离为d1 , 到点F(﹣1,0)的距离为d2 , 且 = .直线l与椭圆C交于不同两点A、B(A,B都在x轴上方),且∠OFA+∠OFB=180°.
20. 已知点P是椭圆C上任一点,点P到直线l1:x=﹣2的距离为d1 , 到点F(﹣1,0)的距离为d2 , 且 = .直线l与椭圆C交于不同两点A、B(A,B都在x轴上方),且∠OFA+∠OFB=180°. (1)、求椭圆C的方程;(2)、当A为椭圆与y轴正半轴的交点时,求直线l方程;(3)、对于动直线l,是否存在一个定点,无论∠OFA如何变化,直线l总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.21. 已知函数f(x)= x2 , g(x)=alnx.(1)、若曲线y=f(x)﹣g(x)在x=1处的切线的方程为6x﹣2y﹣5=0,求实数a的值;(2)、设h(x)=f(x)+g(x),若对任意两个不等的正数x1 , x2 , 都有 >2恒成立,求实数a的取值范围;(3)、若在[1,e]上存在一点x0 , 使得f′(x0)+ <g(x0)﹣g′(x0)成立,求实数a的取值范围.
(1)、求椭圆C的方程;(2)、当A为椭圆与y轴正半轴的交点时,求直线l方程;(3)、对于动直线l,是否存在一个定点,无论∠OFA如何变化,直线l总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.21. 已知函数f(x)= x2 , g(x)=alnx.(1)、若曲线y=f(x)﹣g(x)在x=1处的切线的方程为6x﹣2y﹣5=0,求实数a的值;(2)、设h(x)=f(x)+g(x),若对任意两个不等的正数x1 , x2 , 都有 >2恒成立,求实数a的取值范围;(3)、若在[1,e]上存在一点x0 , 使得f′(x0)+ <g(x0)﹣g′(x0)成立,求实数a的取值范围.