2017年陕西省西安市高考数学一模试卷（理科）

试卷更新日期：2017-04-07 类型：高考模拟

进入出卷网下载

一、选择题：

1. 在复平面内，两共轭复数所对应的点（）

A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、关于直线y=x对称

查看试题解析
2. 已知集合M={﹣1，0，1}，N={x|x=ab，a，b∈M，且a≠b}，则集合M与集合N的关系是（）

A、M=N B、M∩N=N C、M∪N=N D、M∩N=∅

查看试题解析
3. 已知两个单位向量 $\vec{e_{1}} ， \vec{e_{2}}$ 的夹角为45°，且满足 $\vec{e_{1}}$ ⊥（λ $\vec{e_{2}}$ ﹣ $\vec{e_{1}}$ ），则实数λ的值为（）

A、1 B、 $\sqrt{2}$ C、 $\frac{3 \sqrt{3}}{3}$ D、2

查看试题解析
4. 直线x+2y﹣5+ $\sqrt{5}$ =0被圆x²+y²﹣2x﹣4y=0截得的弦长为（）

A、1 B、2 C、4 D、4 $\sqrt{6}$

查看试题解析
5. 将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（　　）

A、12种 B、10种 C、9种 D、8种

查看试题解析
6. 某几何体的三视图如图所示，且该几何体的体积是 $\frac{3}{2}$ ，则正视图中的x的值是（）

A、2 B、 $\frac{9}{2}$ C、 $\frac{3}{2}$ D、3

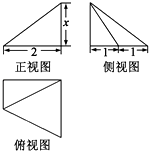查看试题解析
7. 函数y=sin（2x+φ）的图象沿x轴向左平移 $\frac{π}{8}$ 个单位后，得到一个偶函数的图象，则φ的一个可能的值为（）

A、 $\frac{3 π}{4}$ B、 $\frac{π}{4}$ C、0 D、- $\frac{π}{4}$

查看试题解析
8. 公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n值为（）
参考数据： $\sqrt{3} = 1.732$ ，sin15°≈0.2588，sin7.5°≈0.1305．

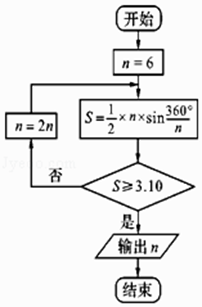A、12 B、24 C、48 D、96

查看试题解析
9. 已知 $α \in R ， \sin α + 2 \cos α = \frac{\sqrt{10}}{2}$ ，则tan2α=（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、﹣ $\frac{3}{4}$ D、- $\frac{4}{3}$

查看试题解析
10. 甲、乙两人约定晚6点到晚7点之间在某处见面，并约定甲若早到应等乙半小时，而乙还有其他安排，若乙早到则不需等待，则甲、乙两人能见面的概率（）

A、 $\frac{3}{8}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
11. F₁、F₂分别是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （a＞0，b＞0）的左、右焦点，过点F₁的直线l与双曲线的左右两支分别交于A、B两点，若△ABF₂是等边三角形，则该双曲线的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
12. 已知函数f（x）=aln（x+1）﹣x²在区间（0，1）内任取两个实数p，q，且p≠q，不等式 $\frac{f (p + 1) - f (q + 1)}{p - q}$ ＞1恒成立，则实数a的取值范围为（）

A、[15，+∞） B、（﹣∞，15] C、（12，30] D、（﹣12，15]

查看试题解析

二、填空题：

13. 已知直线a、b和平面α、β，下列命题中假命题的是（只填序号）．
①若a∥b，则a平行于经过b的任何平面；
②若a∥α，b∥α，则a∥b；
③若a∥α，b∥β，且α⊥β，则a⊥b；
④若α∩β=a，且b∥α，则b∥a．

查看试题解析
14. 有一个游戏，将标有数字1、2、3、4的四张卡片分别随机发给甲、乙、丙、丁4个人，每人一张，并请这4人在看自己的卡片之前进行预测：甲说：乙或丙拿到标有3的卡片；乙说：甲或丙拿到标有2的卡片；丙说：标有1的卡片在甲手中；丁说：甲拿到标有3的卡片．结果显示：这4人的预测都不正确，那么甲、乙、丙、丁4个人拿到的卡片上的数字依次为、、、．

查看试题解析
15. 已知△ABC的顶点A（﹣3，0）和顶点B（3，0），顶点C在椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16}$ =1上，则 $\frac{5 \sin C}{\sin A + \sin B}$ = ．

查看试题解析
16. 定义1：若函数f（x）在区间D上可导，即f′（x）存在，且导函数f′（x）在区间D上也可导，则称函数f（x）在区间D上的存在二阶导数，记作f″（x）=[f′（x）]′．
定义2：若函数f（x）在区间D上的二阶导数恒为正，即f″（x）＞0恒成立，则称函数f（x）在区间D上为凹函数．已知函数f（x）=x³﹣ $\frac{3}{2}$ x²+1在区间D上为凹函数，则x的取值范围是．

查看试题解析

三、解答题：

17. 已知数列{a_n}中，a₃=5，a₅+a₆=20，且2 $^{a_{n}}$ ，2 $^{a_{n + 1}}$ ，2 $^{a_{n + 2}}$ 成等比数列，数列{b_n}满足b_n=a_n﹣（﹣1）ⁿn．
（Ⅰ）求数列{b_n}的通项公式；
（Ⅱ）设s_n是数列{b_n}前n项和，求s_n ．

查看试题解析
18. 某研究小组在电脑上进行人工降雨模拟试验，准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨，其试验数据统计如表
方式
实施地点
大雨
中雨
小雨
模拟实验总次数
A
甲
4次
6次
2次
12次
B
乙
3次
6次
3次
12次
C
丙
2次
2次
8次
12次
假定对甲、乙、丙三地实施的人工降雨彼此互不影响，请你根据人工降雨模拟试验的统计数据
（I）求甲、乙、丙三地都恰为中雨的概率；
（Ⅱ）考虑到旱情和水土流失，如果甲地恰需中雨即达到理想状态，乙地必须是大雨才达到理想状态，丙地只能是小雨或中雨即达到理想状态，记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ，求随机变量ξ的分布列和数学期望Eξ．

查看试题解析
19. 如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D′EC的位置，使D′A=2 $\sqrt{3}$ ，如图＜2＞：若G，H分别为D′B，D′E的中点．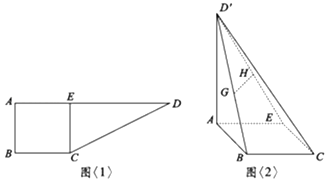

(1)、求证：GH⊥平面AD′C；

(2)、求平面D′AB与平面D′CE的夹角．

查看试题解析
20. 如图，已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的离心率为 $\frac{\sqrt{3}}{2}$ ，以椭圆C的左顶点T为圆心作圆T：（x+2）²+y²=r²（r＞0），设圆T与椭圆C交于点M与点N．

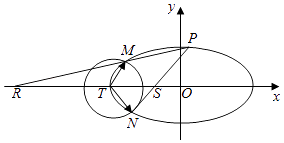(1)、求椭圆C的方程；

(2)、求 $\vec{T M}$ • $\vec{T N}$ 的最小值；

(3)、设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：|OR|•|OS|是定值．

查看试题解析
21. 设函数f（x）=a²lnx+ax（a≠0），g（x）= $\int_{0}^{x}$ 2tdt，F（x）=g（x）﹣f（x）．

(1)、试讨论F（x）的单调性；

(2)、当a＞0时，﹣e²≤F（x）≤1﹣e在x∈[1，e]恒成立，求实数a的取值．

查看试题解析
22. 在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρcos²θ=2sinθ，它在点 $M (2 \sqrt{2} ， \frac{π}{4})$ 处的切线为直线l．

(1)、求直线l的直角坐标方程；

(2)、已知点P为椭圆 $\frac{x^{2}}{3} + \frac{y^{2}}{4}$ =1上一点，求点P到直线l的距离的取值范围．

查看试题解析
23. 已知函数f（x）=|2x﹣1|，x∈R，

(1)、解不等式f（x）＜x+1；

(2)、若对于x，y∈R，有|x﹣y﹣1|≤ $\frac{1}{3}$ ，|2y+1|≤ $\frac{1}{6}$ ，求证：f（x）＜1．

查看试题解析

方式	实施地点	大雨	中雨	小雨	模拟实验总次数
A	甲	4次	6次	2次	12次
B	乙	3次	6次	3次	12次
C	丙	2次	2次	8次	12次