2017年山东省枣庄市高考数学一模试卷（理科）

试卷更新日期：2017-04-07 类型：高考模拟

进入出卷网下载

一、选择题：

1. 若复数z满足（1+i）z=2﹣i（i为虚数单位），则|z|=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{10}}{2}$ C、2 D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析
2. 已知集合A={x|（x+1）（x﹣2）≥0}，B={x|log₃（2﹣x）≤1}，则A∩（∁_RB）=（）

A、∅ B、{x|x≤﹣1，x＞2} C、{x|x＜﹣1} D、{x|x＜﹣1，x≥2}

查看试题解析
3. 函数y=1﹣2sin²（x﹣ $\frac{3 π}{4}$ ）是（）

A、最小正周期为π的奇函数 B、最小正周期为π的偶函数 C、最小正周期为 $\frac{π}{2}$ 的奇函数 D、最小正周期为 $\frac{π}{2}$ 的偶函数

查看试题解析
4. 执行如图所示的程序框图，则输出S的结果为（）

A、2 B、﹣1 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

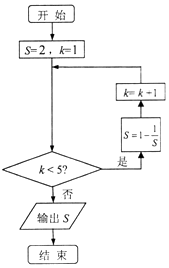查看试题解析
5. 若正数x，y满足 $\frac{1}{y} + \frac{3}{x} = 1$ ，则3x+4y的最小值是（）

A、24 B、28 C、25 D、26

查看试题解析
6. 为了解本市居民的生活成本，甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查．他们将调查所得到的数据分别绘制成频率分布直方图（如图所示），甲、乙、丙所调查数据的标准差分别为x₁ ， x₂ ， x₃ ，则它们的大小关系为（）

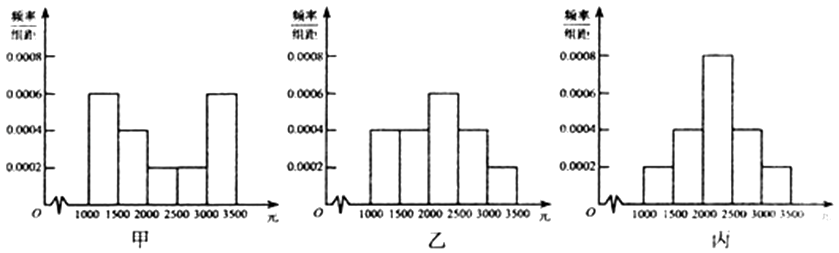A、s₁＞s₂＞s₃ B、s₁＞s₃＞s₂ C、s₃＞s₂＞s₁ D、s₃＞s₁＞s₂

查看试题解析
7. 在△ABC中， $A B = 3 ， A C = 2 ， \vec{B D} = \frac{1}{2} \vec{B C} ，则 \vec{A D} \cdot \vec{D B}$ 的值为（）

A、 $\frac{5}{2}$ B、- $\frac{5}{2}$ C、 $\frac{5}{4}$ D、- $\frac{5}{4}$

查看试题解析
8. 不等式组 ${\begin{matrix} - 1 \leq x \leq 1 \\ 0 \leq y \leq 2 \end{matrix}$ 表示的点集M，不等式组 ${\begin{matrix} x - y + 1 \geq 0 \\ y \geq 2 x^{2} \end{matrix}$ 表示的点集记为N，在M中任取一点P，则P∈N的概率为（）

A、 $\frac{5}{32}$ B、 $\frac{9}{32}$ C、 $\frac{9}{16}$ D、 $\frac{5}{16}$

查看试题解析
9. 已知a∈R，则“a＜0”是“函数f（x）=|x（ax+1）|在（﹣∞，0）上是减函数”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要

查看试题解析
10. 《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著．其中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的四面体称之为鳖膈．已知直三棱柱A₁B₁C₁﹣ABC中，AB⊥BC，AB=3， $B C = 4 ， A A_{1} = 5 \sqrt{3}$ ，将直三棱柱沿一条棱和两个面的对角线分割为一个阳马和一个鳖膈，则鳖膈的体积与其外接球的体积之比为（）

A、 $\sqrt{3} ： 15 π$ B、 $3 \sqrt{3} ： 5 π$ C、 $3 \sqrt{3} ： 50 π$ D、 $3 \sqrt{3} ： 25 π$

查看试题解析

二、填空题：

11. 在 ${(x + \frac{2}{\sqrt{x}})}^{4}$ 的展开式中，x的系数为．（用数字作答）

查看试题解析
12. 已知双曲线C的中心为坐标原点，它的焦点F（2，0）到它的一条渐近线的距离为 $\sqrt{3}$ ，则C的离心率为．

查看试题解析
13. 若“∃x₀∈R，|x₀+1|+|x₀﹣1|≤m”是真命题，则实数m的最小值是．

查看试题解析
14. 某三棱锥的三视图是三个边长相等的正方形及对角线，若该三棱锥的体积是 $\frac{1}{3}$ ，则它的表面积是．

查看试题解析
15. 已知函数f（x）=|x•e^x|，g（x）=f²（x）+λf（x），若方程g（x）=﹣1有且仅有4个不同的实数解，则实数λ的取值范围是．

查看试题解析

三、解答题：

16. 将函数 $y = \sin (x - \frac{π}{3})$ 的图象上每点的横坐标缩短到原来的 $\frac{1}{2}$ 倍（纵坐标不变），得到函数y=f（x）的图象．

(1)、求函数f（x）的解析式及其图象的对称轴方程；

(2)、在△ABC中，内角A，B，C的对边分别为a，b，c．若 $f (A) = \frac{\sqrt{3}}{2} ， a = 2 ， b = \frac{2 \sqrt{3}}{3}$ ，求sinB的值．

查看试题解析
17. 在队内羽毛球选拔赛中，选手M与B₁ ， B₂ ， B₃三位选手分别进行一场对抗赛，按以往多次比赛的统计，M获胜的概率分别为 $\frac{4}{5} ， \frac{2}{3} ， \frac{1}{2}$ ，且各场比赛互不影响．

(1)、若M至少获胜两场的概率大于 $\frac{7}{10}$ ，则M入选下一轮，否则不予入选，问M是否会入选下一轮？

(2)、求M获胜场数X的分布列和数学期望．

查看试题解析
18. 已知等差数列{a_n}的前n项和为S_n ，且a₆=0，S₄=14．

(1)、求a_n；

(2)、将a₂ ， a₃ ， a₄ ， a₅去掉一项后，剩下的三项按原来的顺序恰为等比数列{b_n}的前三项，求数列{a_nb_n}的前n项和T_n ．

查看试题解析
19. 在四边形ABCD中（如图①），AB∥CD，AB⊥BC，G为AD上一点，且AB=AG=1，GD=CD=2，M为GC的中点，点P为边BC上的点，且满足BP=2PC．现沿GC折叠使平面GCD⊥平面ABCG（如图②）．

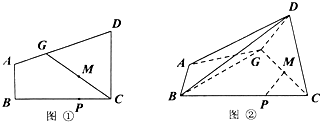(1)、求证：平面BGD⊥平面GCD：

(2)、求直线PM与平面BGD所成角的正弦值．

查看试题解析
20. 已知函数f（x）=x•e^x^﹣¹﹣a（x+lnx），a∈R．

(1)、若曲线y=f（x）在点（1，f（1））处的切线为x轴，求a的值：

(2)、在（1）的条件下，求f（x）的单调区间；

(3)、若∀x＞0，f（x）≥f（m）恒成立，且f（m）≥0，求证：f（m）≥2（m²﹣m³）．

查看试题解析
21. 在平面直角坐标系xOy中，抛物线E：x²=4y的焦点F是椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的一个顶点．过点F且斜率为k（k≠0）的直线l交椭圆C于另一点D，交抛物线E于A、B两点，线段DF的中点为M，直线OM交椭圆C于P、Q两点，记直线OM的斜率为k'，满足 $k \cdot k^{'} = - \frac{1}{4}$ ．

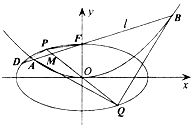(1)、求椭圆C的方程；

(2)、记△PDF的面积为S₁ ， △QAB的面积为S₂ ，设 $S_{1} \cdot S_{2} = λ k^{2}$ ，求实数λ的最大值及取得最大值时直线l的方程．

查看试题解析