2017年山东省日照市高考数学一模试卷（理科）

试卷更新日期：2017-04-07 类型：高考模拟

进入出卷网下载

一、选择题：

1. 已知集合M={0，1，2}，N={x|﹣1≤x≤1，x∈Z}，则（）

A、M⊆N B、N⊆M C、M∩N={0，1} D、M∪N=N

查看试题解析
2. 如果复数z= $\frac{3 - b i}{2 + i}$ （b∈R）的实部和虚部相等，则|z|等于（）

A、3 $\sqrt{2}$ B、2 $\sqrt{2}$ C、3 D、2

查看试题解析
3. “log₂（2x﹣3）＜1”是“4^x＞8”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 函数y=x²+ln|x|的图象大致为（）

A、 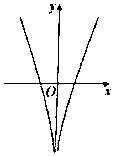B、 C、 D、

查看试题解析
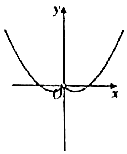5. 函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，﹣π＜φ＜0）的部分图象如图所示，为了得到g（x）=Asinωx的图象，只需将函数y=f（x）的图象（）

A、向左平移 $\frac{π}{6}$ 个单位长度 B、向左平移 $\frac{π}{12}$ 个单位长度 C、向右平移 $\frac{π}{6}$ 个单位长度 D、向右平移 $\frac{π}{12}$ 个单位长度

查看试题解析
6. 甲、乙、丙 3人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法总数是（）

A、210 B、84 C、343 D、336

查看试题解析
7. 已知变量x，y满足： ${\begin{matrix} 2 x - y \leq 0 \\ x - 2 y + 3 \geq 0 \\ x \geq 0 \end{matrix}$ ，则z=（ $\sqrt{2}$ ）^2x⁺^y的最大值为（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、2 D、4

查看试题解析
8. 公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为（）
（参考数据： $\sqrt{3}$ ≈1.732，sin15°≈0.2588，sin7.5°≈0.1305）

A、12 B、24 C、36 D、48

查看试题解析
9. 已知O为坐标原点，F是双曲线 $Γ ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点，A，B分别为Γ的左、右顶点，P为Γ上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E，直线 BM与y轴交于点N，若|OE|=2|ON|，则 Γ的离心率为（）

A、3 B、2 C、 $\frac{3}{2}$ D、 $\frac{4}{3}$

查看试题解析
10. 曲线 $y = \frac{x^{2} + 4}{x}$ 的一条切线l与y=x，y轴三条直线围成三角形记为△OAB，则△OAB外接圆面积的最小值为（）

A、 $8 \sqrt{2} π$ B、 $8 (3 - \sqrt{2}) π$ C、 $16 (\sqrt{2} - 1) π$ D、 $16 (2 - \sqrt{2}) π$

查看试题解析

二、填空题：

11. 设 ${(2 x^{2} + 1)}^{5} = a_{0} + a_{1} x^{2} + a_{2} x^{4} + \dots + a_{5} x^{10} ，则 a_{3}$ 的值为．

查看试题解析
12. 设随机变量ξ服从正态分布N（2，9），若P（ξ＞c+1）=P（ξ＜c﹣1），则c= ．

查看试题解析
13. 现有一半球形原料，若通过切削将该原料加工成一正方体工件，则所得工件体积与原料体积之比的最大值为．

查看试题解析
14. 有下列各式： $1 + \frac{1}{2} + \frac{1}{3} > 1$ ， $1 + \frac{1}{2} + \dots + \frac{1}{7} > \frac{3}{2}$ ， $1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{15} > 2$ ，…则按此规律可猜想此类不等式的一般形式为：．

查看试题解析
15. 在 $△ A B C 中， ∠ A = \frac{π}{3} ，且 (\vec{A B} + \vec{A C}) \cdot \vec{B C} = 0$ ，点M是△ABC外一点，BM=2CM=2，则AM的最大值与最小值的差为．

查看试题解析

三、解答题：

16. 已知函数f（x）= $\sqrt{3}$ sin2x﹣2cos²x﹣1，x∈R．
（Ⅰ）求函数f（x）的最小正周期和最小值；
（Ⅱ）在△ABC中，A，B，C的对边分别为a，b，c，已知c= $\sqrt{3}$ ，f（C）=0，sinB=2sinA，求a，b的值．

查看试题解析
17. 一袋中有7个大小相同的小球，其中有2个红球，3个黄球，2个蓝球，从中任取3个小球．

（I）求红、黄、蓝三种颜色的小球各取1个的概率；
（II）设X表示取到的蓝色小球的个数，求X的分布列和数学期望．

查看试题解析
18. 如图，菱形ABCD与正三角形BCE的边长均为2，它们所在平面互相垂直，FD⊥平面ABCD，且FD= $\sqrt{3}$ ．
（I）求证：EF∥平面ABCD；
（Ⅱ）若∠CBA=60°，求二面角A﹣FB﹣E的余弦值．

查看试题解析
19. 已知数列{a_n}满足a₁=1，a_n₊₁=1﹣ $\frac{1}{4 a_{n}}$ ，其中n∈N^* ．
（Ⅰ）设b_n= $\frac{2}{2 a_{n} - 1}$ ，求证：数列{b_n}是等差数列，并求出{a_n}的通项公式a_n；
（Ⅱ）设C_n= $\frac{4 a_{n}}{n + 1}$ ，数列{C_nC_n₊₂}的前n项和为T_n ，是否存在正整数m，使得T_n＜ $\frac{1}{C_{m} C_{m + 1}}$ 对于n∈N^*恒成立，若存在，求出m的最小值，若不存在，请说明理由．

查看试题解析
20. 已知左、右焦点分别为F₁（﹣c，0），F₂（c，0）的椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $(\sqrt{3} ， \frac{\sqrt{3}}{2})$ ，且椭圆C关于直线x=c对称的图形过坐标原点．
（I）求椭圆C的离心率和标准方程．
（II）圆 $P_{1} ： {(x + \frac{4 \sqrt{3}}{7})}^{2} + {(y - \frac{3 \sqrt{3}}{7})}^{2} = r^{2} (r > 0)$ 与椭圆C交于A，B两点，R为线段AB上任一点，直线F₁R交椭圆C于P，Q两点，若AB为圆P₁的直径，且直线F₁R的斜率大于1，求|PF₁||QF₁|的取值范围．

查看试题解析
21. 设f（x）=xe^x（e为自然对数的底数），g（x）=（x+1）² ．
（I）记 $F (x) = \frac{f (x)}{g (x)}$ ，讨论函F（x）单调性；
（II）令G（x）=af（x）+g（x）（a∈R），若函数G（x）有两个零点．
（i）求参数a的取值范围；
（ii）设x₁ ， x₂是G（x）的两个零点，证明x₁+x₂+2＜0．

查看试题解析