安徽省滁州市定远县西片区2018-2019学年高一上学期数学期中考试试卷

试卷更新日期：2018-12-29 类型：期中考试

进入出卷网下载

一、单选题

1. 对于任意两个正整数m，n，定义某种运算“※”如下：当m，n都为正偶数或正奇数时，m※n＝m＋n；当m，n中一个为正偶数，另一个为正奇数时，m※n＝mn，则在此定义下，集合M＝{(a，b)|a※b＝16}中的元素个数是（）

A、18 B、17 C、16 D、15

查看试题解析
2. 已知集合 $A = {x | y = ln (x + 3)}$ ， $B = {x | x \geq 2}$ ，则下列结论正确的是（）

A、 B、 C、 D、

查看试题解析
3. 已知全集U={1，2，3，4，5，6}，集合P={1，3，5}，Q={1，2，4}，则 $(∁_{U} P) \cup^{} Q$ =（）

A、{1} B、{3，5} C、{1，2，4，6} D、{1，2，3，4，5}

查看试题解析
4. 函数y＝ $\sqrt{x (x - 1)}$ ＋lnx的定义域为（）

A、{x|x>0} B、{x|x≥1} C、{x|x>1} D、{x|0<x≤1}

查看试题解析
5. 已知a，b为两个不相等的实数，集合M＝{a²－4a，－1}，N＝{b²－4b＋1，－2}，映射f：x→x表示把集合M中的元素x映射到集合N中仍为x，则a＋b等于（）

A、1 B、2 C、3 D、4

查看试题解析
6. 已知f（x）是定义在R上的偶函数，且在（0，+∞）上是增函数，设a=f（﹣ $\sqrt{3}$ ），b=f（log₃ $\frac{1}{2}$ ），c=f（ $\frac{4}{3}$ ），则a、b、c的大小关系是（　　）

A、a＜c＜b B、b＜a＜c C、b＜c＜a D、c＜b＜a

查看试题解析
7. 已知函数 $f (x) = {\begin{cases} x^{2} + 2 x ， x < 0 \\ x^{2} - 2 x ， x \geq 0 \end{cases}$ .若 $f (- a) + f (a) \leq 0$ ，则 $a$ 的取值范围是（）

A、 B、 C、 D、

查看试题解析
8. 已知函数f(x)＝x²＋ax＋4，若对任意的x∈(0，2]，f(x)≤6恒成立，则实数a的最大值为（）

A、－1 B、1 C、－2 D、2

查看试题解析
9. 已知幂函数 $f (x) ＝ (n^{2} ＋ 2 n － 2) x^{n^{2} － 3 n}$ (n∈Z)的图象关于y轴对称，且在(0，＋∞)上是减函数，则n的值为（）

A、－3 B、1 C、2 D、1或2

查看试题解析
10. 已知a>0，且a≠1，函数 $y = a^{x}$ 与y＝log_a(－x)的图象只能是下图中的（）

A、 B、 C、 D、

查看试题解析
11. 已知x，y，z都是大于1的正数，m>0，且log_xm＝24，log_ym＝40，log_xyzm＝12，则log_zm的值为（）

A、 B、60 C、 D、

查看试题解析
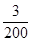12. 已知幂函数f(x)＝ $x^{－ \frac{1}{2}}$ ，若f(a＋1)<f(10－2a)，则a的取值范围是（）

A、(3，5) B、(－1，＋∞) C、(－∞，5) D、(－1，5)

查看试题解析

二、填空题

13. 若幂函数y＝(m²＋3m＋3) $x^{m^{2} ＋ 2 m － 3}$ 的图象不过原点，且关于原点对称，则m＝.

查看试题解析
14. 已知f(x⁵)＝log₂x，则f(2)＝.

查看试题解析
15. 化简 $\frac{a^{\frac{2}{3}} \sqrt{b}}{a^{- \frac{1}{2}} \cdot \sqrt[3]{b}} \div {(\frac{a^{- 1} \sqrt{b^{- 1}}}{b \sqrt{a}})}^{- \frac{2}{3}}$ 的值为．

查看试题解析
16. 已知函数 $f (x) = {log}_{a} x$ a>0且a≠1)的图象过点P(4， $\frac{1}{2}$ )，则f(x)的解析式为．

查看试题解析

三、解答题

17. 设A为实数集，且满足条件：若a∈A，则 $\frac{1}{1 - a}$ ∈A(a≠1)．
求证：

(1)、若2∈A，则A中必还有另外两个元素；

(2)、集合A不可能是单元素集．

查看试题解析
18. 定义在R上的奇函数f(x)满足f(x＋2)＝－f(x)，当0≤x≤1时，f(x)＝x，

(1)、试画出f(x)，x∈[－3，5]的图象；

(2)、求f(37.5)；

(3)、常数a∈(0，1)，y＝a与f(x)，x∈[－3，5]的图象相交，求所有交点横坐标之和．

查看试题解析
19. 某公司计划投资A、B两种金融产品，根据市场调查与预测，A产品的利润与投资量成正比例，其关系如图1，B产品的利润与投资量的算术平方根成正比例，其关系如图2(注：利润与投资量的单位：万元)．

(1)、分别将A、B两产品的利润表示为投资量的函数关系式；

(2)、该公司已有10万元资金，并全部投入A、B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？

查看试题解析
20. 记函数f(x)＝ $\frac{1}{\sqrt{2 x - 3}}$ 的定义域为集合A，函数g(x)＝ $\frac{k - 1}{x}$ 在(0，＋∞)上为增函数时k的取值集合为B，函数h(x)＝x²＋2x＋4的值域为集合C．

(1)、求集合A，B，C；

(2)、求集合A∪(∁_RB)，A∩(B∪C)．

查看试题解析
21. 已知f(x)＝x²＋(a＋1)x＋a²(a∈R)，若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和．

(1)、求g(x)和h(x)的解析式；

(2)、若f(x)和g(x)在区间(－∞，(a＋1)²]上都是减函数，求f(1)的取值范围．

查看试题解析
22. 已知函数f(x)是定义在R上的奇函数，且当x≥0时，f(x)＝ $\frac{2 x}{x + 2}$ .

(1)、求f(x)的解析式；

(2)、判断f(x)的单调性；

(3)、若对任意的t∈R，不等式f(k－3t²)＋f(t²＋2t)≤0恒成立，求k的取值范围.

查看试题解析