安徽省定远重点中学2018-2019学年高二上学期理数期中考试试卷
试卷更新日期:2018-12-29 类型:期中考试
一、单选题
-
1. 已知命题 , ;命题 ,使 则下列命题中为真命题的是( )A、
 B、p∧(
B、p∧(  q)
q)  C、
C、 D、
D、 2. 下列说法正确的是( )A、命题“
2. 下列说法正确的是( )A、命题“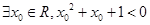 ”的否定是:“
”的否定是:“ 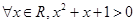 ”
B、“
”
B、“ 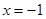 ”是“
”是“ 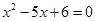 ”的必要不充分条件
C、命题“若
”的必要不充分条件
C、命题“若 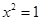 ,则
,则 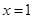 ”的否命题是:若
”的否命题是:若 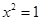 ,则
,则 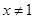 D、命题“若 ,则
D、命题“若 ,则 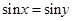 ”的逆否命题为真命题.
3. 设定点 、 ,动点 满足 ,则点 的轨迹是( )A、椭圆 B、线段 C、不存在 D、椭圆或线段4. 设 分别是椭圆 的左,右焦点, 是椭圆上一点,且 则 的面积为( )A、24 B、25 C、30 D、405. 在平面直角坐标系 中,已知 为函数 图象上一点,若 ,则 ( )A、
”的逆否命题为真命题.
3. 设定点 、 ,动点 满足 ,则点 的轨迹是( )A、椭圆 B、线段 C、不存在 D、椭圆或线段4. 设 分别是椭圆 的左,右焦点, 是椭圆上一点,且 则 的面积为( )A、24 B、25 C、30 D、405. 在平面直角坐标系 中,已知 为函数 图象上一点,若 ,则 ( )A、 B、
B、 C、
D、
6. 设双曲线 的中心为点 ,若直线 和 相交于点 ,直线 交双曲线于 ,直线 交双曲线于 ,且使 则称 和 为“ 直线对”.现有所成的角为60°的“ 直线对”只有2对,且在右支上存在一点 ,使 ,则该双曲线的离心率的取值范围是( )A、
C、
D、
6. 设双曲线 的中心为点 ,若直线 和 相交于点 ,直线 交双曲线于 ,直线 交双曲线于 ,且使 则称 和 为“ 直线对”.现有所成的角为60°的“ 直线对”只有2对,且在右支上存在一点 ,使 ,则该双曲线的离心率的取值范围是( )A、 B、
B、 C、
C、 D、
D、 7. 已知双曲线 的右顶点为 ,以 为圆心, 为半径作圆 ,圆 与双曲线 的一条渐近线交于 , 两点,若 ,则 的离心率为( )A、 B、 C、2 D、
7. 已知双曲线 的右顶点为 ,以 为圆心, 为半径作圆 ,圆 与双曲线 的一条渐近线交于 , 两点,若 ,则 的离心率为( )A、 B、 C、2 D、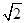 8. 已知 为坐标原点, , 是双曲线 : ( , )的左、右焦点,双曲线 上一点 满足 ,且 ,则双曲线 的离心率为( )A、 B、2 C、 D、
8. 已知 为坐标原点, , 是双曲线 : ( , )的左、右焦点,双曲线 上一点 满足 ,且 ,则双曲线 的离心率为( )A、 B、2 C、 D、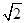 9. 已知点 是抛物线 上的一点,设点 到此抛物线准线的距离为 ,到直线 的距离为 ,则 的最小值为 ( )A、4 B、
9. 已知点 是抛物线 上的一点,设点 到此抛物线准线的距离为 ,到直线 的距离为 ,则 的最小值为 ( )A、4 B、 C、5
D、
C、5
D、 10. 已知点 在抛物线 上,则当点 到点 的距离与点 到抛物线焦点距离之和取得最小值时,点 的坐标为( )A、
10. 已知点 在抛物线 上,则当点 到点 的距离与点 到抛物线焦点距离之和取得最小值时,点 的坐标为( )A、 B、
B、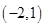 C、
C、 D、
D、 11. 过曲线 图象上一点(2, 2)及邻近一点(2 , 2 )作割线,则当 时割线的斜率为( )A、
11. 过曲线 图象上一点(2, 2)及邻近一点(2 , 2 )作割线,则当 时割线的斜率为( )A、 B、
C、1
D、
12. 已知 ,则 ( )A、 B、 C、 D、以上都不正确
B、
C、1
D、
12. 已知 ,则 ( )A、 B、 C、 D、以上都不正确二、填空题
-
13. 关于 的不等式 成立的充分不必要条件是 ,则实数 的取值范围是 .14. 已知圆 : 及一点 , 在圆 上运动一周, 的中点 形成轨迹 的方程为 .
15. 直线 与椭圆 交与 两点,以线段 为直径的圆恰好经过椭圆的右焦点,则椭圆 的离心率为 .16. 已知在 上可导, ,则 .三、解答题
-
17. 已知 是定义在 上的奇函数,当 时, ,且曲线 在 处的切线与直线 平行.
(Ⅰ)求 的值及函数 的解析式;
(Ⅱ)若函数 在区间 上有三个零点,求实数 的取值范围.
18. 已知函数 .(Ⅰ)若函数 在 处的切线方程为 ,求 和 的值;
(Ⅱ)讨论方程 的解的个数,并说明理由.
19. 已知抛物线 的焦点为 是过F的直线与抛物线的两个交点,求证:
(1)、y1y2=-p2 , ;(2)、 为定值;(3)、以AB为直径的圆与抛物线的准线相切.20. 已知 分别是双曲线E: 的左、右焦点,P是双曲线上一点, 到左顶点的距离等于它到渐近线距离的2倍(1)、求双曲线的渐近线方程;(2)、当 时, 的面积为 ,求此双曲线的方程。
