安徽省滁州市定远县西片区2018-2019学年高二上学期理数期中考试试卷
试卷更新日期:2018-12-29 类型:期中考试
一、单选题
-
1. 光线沿着直线 射到直线 上,经反射后沿着直线 射出,则由( )A、
 ,
,  B、
B、 ,
,  C、 ,
C、 ,  D、
D、 ,
,  2. 若圆 的圆心到直线 的距离为 ,则 的值为( ).A、
2. 若圆 的圆心到直线 的距离为 ,则 的值为( ).A、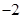 或
或  B、 或
C、
B、 或
C、 或
或 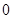 D、
D、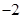 或
或 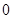 3. 在三棱柱 中, 是等边三角形, 平面 ,则异面直线 和 所成角的正弦值为( )
3. 在三棱柱 中, 是等边三角形, 平面 ,则异面直线 和 所成角的正弦值为( ) A、1 B、
A、1 B、 C、
D、
4. 某几何体的三视图如图所示,则该几何体的体积是( )
C、
D、
4. 某几何体的三视图如图所示,则该几何体的体积是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 在四面体 中, 底面 , , , , 为 的重心, 为线段 上一点,且 平面 ,则线段 的长为( )A、 B、 C、
5. 在四面体 中, 底面 , , , , 为 的重心, 为线段 上一点,且 平面 ,则线段 的长为( )A、 B、 C、 D、
6. 如图4,正三棱柱 中,各棱长都相等,则二面角 的平面角的正切值为( )
D、
6. 如图4,正三棱柱 中,各棱长都相等,则二面角 的平面角的正切值为( ) A、
A、 B、
C、1
D、
B、
C、1
D、 7. 如图,三棱柱ABC-A1B1BC1中,侧棱AA1⊥底面A1B1C1 , 底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
7. 如图,三棱柱ABC-A1B1BC1中,侧棱AA1⊥底面A1B1C1 , 底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( ) A、CC1与B1E是异面直线 B、AC⊥平面ABB1A1 C、AE⊥B1C D、A1C1//平面AB1E8. 已知圆 与直线 及 都相切,圆心在直线 上,则圆 的方程为( )A、
A、CC1与B1E是异面直线 B、AC⊥平面ABB1A1 C、AE⊥B1C D、A1C1//平面AB1E8. 已知圆 与直线 及 都相切,圆心在直线 上,则圆 的方程为( )A、 B、
B、 C、
C、 D、
D、 9. 在三棱锥 中, 与 都是边长为 的正三角形,平面 平面 ,则该三棱锥的外接球的体积为( )A、
9. 在三棱锥 中, 与 都是边长为 的正三角形,平面 平面 ,则该三棱锥的外接球的体积为( )A、 B、
B、 C、
C、 D、
D、 10. 一个几何体的三视图如图所示,其中俯视图为正方形,则该几何体最大的侧面的面积为
10. 一个几何体的三视图如图所示,其中俯视图为正方形,则该几何体最大的侧面的面积为 A、
A、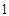 B、
C、
D、2
11. 若直线 与曲线 有两个交点,则实数 的取值范围是( )A、
B、
C、
D、2
11. 若直线 与曲线 有两个交点,则实数 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 12. 设 为两个不重合的平面, 为两两不重合的直线,给出下列四个命题:
12. 设 为两个不重合的平面, 为两两不重合的直线,给出下列四个命题:①若 , ,则 ;②若 , , , ,则 ;③若 , ,则 ;④若 , ,且 , ,则 .
其中正确命题的序号是( )
A、①③ B、①②③ C、①③④ D、②④二、填空题
-
13. 如图,半球内有一内接正四棱锥 ,该四棱锥的体积为 ,则该半球的表面积为 .
 14. 已知 的顶点都在球 的球面上, ,三棱锥 的体积为 ,则该球的表面积等于.15. 如图,已知AB为圆O的直径,C为圆上一动点, 圆O所在平面,且PA=AB=2,过点A作平面 ,交PB,PC分别于E,F,当三棱锥P-AEF体积最大时, = .
14. 已知 的顶点都在球 的球面上, ,三棱锥 的体积为 ,则该球的表面积等于.15. 如图,已知AB为圆O的直径,C为圆上一动点, 圆O所在平面,且PA=AB=2,过点A作平面 ,交PB,PC分别于E,F,当三棱锥P-AEF体积最大时, = . 16. 在平面直角坐标系中, 分别是 轴和 轴上的动点,若以 为直径的圆 与直线 相切,则圆 面积的最小值为 .
16. 在平面直角坐标系中, 分别是 轴和 轴上的动点,若以 为直径的圆 与直线 相切,则圆 面积的最小值为 .三、解答题
-
17. 直线过点P 且与x轴、y轴的正半轴分别交于A , B两点,O为坐标原点,是否存在这样的直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6.若存在,求出方程;若不存在,请说明理由.18. 在平面直角坐标系中,圆 : 与 轴的正半轴交于点 ,以 为圆心的圆 : ( )与圆 交于 , 两点.
 (1)、若直线 与圆 切于第一象限,且与坐标轴交于 , ,当直线 长最小时,求直线 的方程;(2)、设 是圆 上异于 , 的任意一点,直线 、 分别与 轴交于点 和 ,问 是否为定值?若是,请求出该定值;若不是,请说明理由.19. 如下图,在四棱锥 中,底面 是边长为 的正方形,侧棱 底面 ,且侧棱 的长是 ,点 分别是 的中点.
(1)、若直线 与圆 切于第一象限,且与坐标轴交于 , ,当直线 长最小时,求直线 的方程;(2)、设 是圆 上异于 , 的任意一点,直线 、 分别与 轴交于点 和 ,问 是否为定值?若是,请求出该定值;若不是,请说明理由.19. 如下图,在四棱锥 中,底面 是边长为 的正方形,侧棱 底面 ,且侧棱 的长是 ,点 分别是 的中点.
(Ⅰ)证明: 平面 ;
(Ⅱ)求三棱锥 的体积.


