2017年辽宁省丹东市、鞍山市、营口市高考数学一模试卷（理科）23

试卷更新日期：2017-04-06 类型：高考模拟

进入出卷网下载

一、选择题

1. 设P={x|x＜4}，Q={x|x²＜4}，则（）

A、P⊆Q B、Q⊆P C、P⊆∁_RQ D、Q⊆∁_RP

查看试题解析
2. 复数 $\frac{2 - m i}{1 + 2 i} = A + B i ， (m ， A ， B \in R)$ ，且A+B=0，则m的值是（）

A、 $\sqrt{2}$ B、 $\frac{2}{3}$ C、﹣ $\frac{2}{3}$ D、2

查看试题解析
3. 设样本数据x₁ ， x₂ ， …，x₁₀的均值和方差分别为1和4，若y_i=x_i+a（a为非零常数，i=1，2，…，10），则y₁ ， y₂ ， …，y₁₀的均值和方差分别为（）

A、1+a，4 B、1+a，4+a C、1，4 D、1，4+a

查看试题解析
4. 公差不为零的等差数列{a_n}的前n项和为S_n ．若a₄是a₃与a₇的等比中项，S₈=32，则S₁₀等于（　　）

A、18 B、24 C、60 D、90

查看试题解析
5. 设F₁和F₂为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （a＞0，b＞0）的两个焦点，若F₁ ， F₂ ， P（0，2b）是正三角形的三个顶点，则双曲线的渐近线方程是（）

A、y=± $\frac{\sqrt{3}}{3}$ x B、y=± $\sqrt{3}$ x C、y=± $\frac{\sqrt{21}}{7}$ x D、y=± $\frac{\sqrt{21}}{3}$ x

查看试题解析
6. 设a=log₂3， $b = \frac{4}{3}$ ，c=log₃4，则a，b，c的大小关系为（）

A、b＜a＜c B、c＜a＜b C、a＜b＜c D、c＜b＜a

查看试题解析
7. 圆x²+y²﹣4x﹣4y﹣10=0上的点到直线x+y﹣8=0的最大距离与最小距离的差是（）

A、18 B、6 $\sqrt{2}$ C、5 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析
8. 已知某几何体的三视图如图所示，则该几何体的体积为（）

A、 $\frac{8 π}{3}$ B、3π C、 $\frac{10 π}{3}$ D、6π

查看试题解析
9. （x+y+z）⁴的展开式共（）项．

A、10 B、15 C、20 D、21

查看试题解析
10. 为了竖一块广告牌，要制造三角形支架，如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了稳固广告牌，要求AC越短越好，则AC最短为（　　）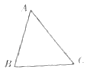

A、（1+ $\frac{\sqrt{3}}{2}$ ）米 B、2米 C、（1+ $\sqrt{3}$ ）米 D、（2+ $\sqrt{3}$ ）米

查看试题解析
11. 已知函数f（x）在R上满足f（x）=2f（2﹣x）﹣x²+8x﹣8，则曲线y=f（x）在点（1，f（1））处的切线方程是（）

A、y=﹣2x+3 B、y=x C、y=3x﹣2 D、y=2x﹣1

查看试题解析
12. 已知椭圆的左焦点为F₁ ，有一小球A从F₁处以速度v开始沿直线运动，经椭圆壁反射（无论经过几次反射速度大小始终保持不变，小球半径忽略不计），若小球第一次回到F₁时，它所用的最长时间是最短时间的5倍，则椭圆的离心率为（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

13. 等比数列{a_n}的公比q＞0．已知a₂=1，a_n₊₂+a_n₊₁=6a_n ，则{a_n}的前4项和S₄= ．

查看试题解析
14. 如图所示，输出的x的值为．

查看试题解析
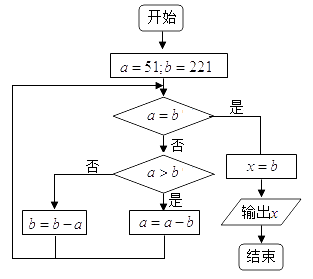15. 已知四面体ABCD，AB=4，AC=AD=6，∠BAC=∠BAD=60°，∠CAD=90°，则该四面体外接球半径为．

查看试题解析
16. 设点P在曲线y= $\frac{1}{2}$ e^x上，点Q在曲线y=ln（2x）上，则|PQ|的最小值为．

查看试题解析

三、解答题

17. 已知函数f（x）=2cos²x+2 $\sqrt{3}$ sinxcosx+a，且当x∈[0， $\frac{π}{2}$ ]时，f（x）的最小值为2．

(1)、求a的值，并求f（x）的单调递增区间；

(2)、先将函数y=f（x）的图象上的点纵坐标不变，横坐标缩小到原来的 $\frac{1}{2}$ ，再将所得图象向右平移 $\frac{π}{12}$ 个单位，得到函数y=g（x）的图象，求方程g（x）=4在区间[0， $\frac{π}{2}$ ]上所有根之和．

查看试题解析
18. 某校举行“庆元旦”教工羽毛球单循环比赛（任意两个参赛队只比赛一场），共有高一、高二、高三三个队参赛，高一胜高二的概率为 $\frac{1}{2}$ ，高一胜高三的概率为 $\frac{2}{3}$ ，高二胜高三的概率为P，每场胜负独立，胜者记1分，负者记0分，规定：积分相同者高年级获胜．

（Ⅰ）若高三获得冠军概率为 $\frac{1}{3}$ ，求P．
（Ⅱ）记高三的得分为X，求X的分布列和期望．

查看试题解析
19. 如图所示，三棱柱ABC﹣A₁B₁C₁中，已知AB⊥侧面BB₁C₁C，AB=BC=1，BB₁=2，∠BCC₁=60°．
（Ⅰ）求证：C₁B⊥平面ABC；
（Ⅱ）E是棱CC₁所在直线上的一点，若二面角A﹣B₁E﹣B的正弦值为 $\frac{1}{2}$ ，求CE的长．

查看试题解析
20. 已知抛物线C：y=2x² ，直线l：y=kx+2交C于A，B两点，M是线段AB的中点，过M作x轴的垂线C于点N．

(1)、证明：抛物线C在点N处的切线与AB平行；

(2)、是否存在实数k使以AB为直径的圆M经过点N，若存在，求k的值，若不存在，说明理由．

查看试题解析
21. 已知函数f（x）=x²+ $\frac{2}{x}$ +alnx．

（Ⅰ）若f（x）在区间[2，3]上单调递增，求实数a的取值范围；
（Ⅱ）设f（x）的导函数f′（x）的图象为曲线C，曲线C上的不同两点A（x₁ ， y₁）、B（x₂ ， y₂）所在直线的斜率为k，求证：当a≤4时，|k|＞1．

查看试题解析
22. 选修4﹣4；坐标系与参数方程
已知曲线C₁的参数方程是 ${\begin{matrix} x = 2 \cos ϕ \\ y = 3 \sin ϕ \end{matrix}$ （φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C₂的坐标系方程是ρ=2，正方形ABCD的顶点都在C₂上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2， $\frac{π}{3}$ ）．

(1)、求点A，B，C，D的直角坐标；

(2)、设P为C₁上任意一点，求|PA|²+|PB|²+|PC|²+|PD|²的取值范围．

查看试题解析
23. 设不等式﹣2＜|x﹣1|﹣|x+2|＜0的解集为M，a、b∈M，

(1)、证明：| $\frac{1}{3}$ a+ $\frac{1}{6}$ b|＜ $\frac{1}{4}$ ；

(2)、比较|1﹣4ab|与2|a﹣b|的大小，并说明理由．

查看试题解析