2017年河南省新乡市高考数学二模试卷（理科）

试卷更新日期：2017-04-06 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合A={x|x（x﹣2）=0}，B={x∈Z|4x²﹣9≤0}，则A∪B等于（）

A、{﹣2，﹣1，0，1} B、{﹣1，0，1，2} C、[﹣2，2] D、{0，2}

查看试题解析
2. 设a∈R，若复数z= $\frac{a - i}{3 + i}$ （i是虚数单位）的实部为2，则复数z的虚部为（）

A、7 B、﹣7 C、1 D、﹣1

查看试题解析
3. 已知向量 $\vec{a}$ =（1，2）， $\vec{b}$ =（m，﹣4），若| $\vec{a}$ || $\vec{b}$ |+ $\vec{a}$ • $\vec{b}$ =0，则实数m等于（）

A、﹣4 B、4 C、﹣2 D、2

查看试题解析
4. 设a=6^0.4 ， b=log_0.40.5，c=log₈0.4，则a，b，c的大小关系是（）

A、a＜b＜c B、c＜b＜a C、c＜a＜b D、b＜c＜a

查看试题解析
5. 执行如图所示的程序框图，输出S的值为（）

A、﹣ $\frac{31}{15}$ B、﹣ $\frac{7}{5}$ C、﹣ $\frac{31}{17}$ D、﹣ $\frac{21}{17}$

查看试题解析
6. 已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示，为了解该小区户主对户型结构的满意程度，用分层抽样的方法抽取20%的户主进行调查，则样本容量和抽取的户主对四居室满意的人数分别为（）

A、100，8 B、80，20 C、100，20 D、80，8

查看试题解析
7. 已知双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的右焦点为F，点B是虚轴上的一个顶点，线段BF与双曲线C的右支交于点A，若 $\vec{B A}$ =2 $\vec{A F}$ ，且| $\vec{B F}$ |=4，则双曲线C的方程为（）

A、 $\frac{x^{2}}{6}$ ﹣ $\frac{y^{2}}{5}$ =1 B、 $\frac{x^{2}}{8}$ ﹣ $\frac{y^{2}}{12}$ =1 C、 $\frac{x^{2}}{8}$ ﹣ $\frac{y^{2}}{4}$ =1 D、 $\frac{x^{2}}{4}$ ﹣ $\frac{y^{2}}{6}$ =1

查看试题解析
8. 已知一个几何体的三视图如图所示，则该几何体的体积为（）

A、 $\frac{32}{3}$ B、 $\frac{16}{3}$ C、 $\frac{8}{3}$ D、 $\frac{4}{3}$

查看试题解析
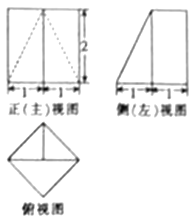9. 设函数f（x）=sin（2x+ $\frac{π}{4}$ ）（x∈[0， $\frac{9 π}{8}$ ]），若方程f（x）=a恰好有三个根，分别为x₁ ， x₂ ， x₃（x₁＜x₂＜x₃），则x₁+x₂+x₃的取值范围是（）

A、[ $\frac{9 π}{8}$ ， $\frac{5 π}{4}$ ） B、[ $\frac{5 π}{4}$ ， $\frac{11 π}{8}$ ） C、[ $\frac{3 π}{2}$ ， $\frac{13 π}{8}$ ） D、[ $\frac{7 π}{4}$ ， $\frac{15 π}{8}$ ）

查看试题解析
10. 若实数x，y满足 ${\begin{matrix} 2 x - y + 2 \geq 0 \\ 2 x + y - 6 \leq 0 \\ 0 \leq y \leq 3 \end{matrix}$ ，且z=mx﹣y（m＜2）的最小值为﹣ $\frac{5}{2}$ ，则m等于（）

A、 $\frac{5}{4}$ B、﹣ $\frac{5}{6}$ C、1 D、 $\frac{1}{3}$

查看试题解析
11. 已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O﹣ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（）

A、 $\frac{15 π}{4}$ B、4π C、 $\frac{7 π}{2}$ D、3π

查看试题解析
12. 函数y=f（x）图象上不同两点A（x₁ ， y₁），B（x₂ ， y₂）处的切线的斜率分别是k_A ， k_B ，规定φ（A，B）= $\frac{| k_{A} - k_{B} |}{| A B |}$ 叫做曲线在点A与点B之间的“弯曲度”．设曲线y=e^x上不同的两点A（x₁ ， y₁），B（x₂ ， y₂），且x₁﹣x₂=1，若t•φ（A，B）＜3恒成立，则实数t的取值范围是（）

A、（﹣∞，3] B、（﹣∞，2] C、（﹣∞，1] D、[1，3]

查看试题解析

二、填空题

13. 若（1﹣2x）⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵ ，则 $\frac{a_{^{3}}}{a_{2}}$ = ．

查看试题解析
14. 已知点A（1，y₁），B（9，y₂）是抛物线y²=2px（p＞0）上的两点，y₂＞y₁＞0，点F是它的焦点，若|BF|=5|AF|，则y₁²+y₂的值为．

查看试题解析
15. 我国古代数学著作《九章算术》有如下问题：“今有人持金出五关，前关二而税一，次关三而税一，次关四而税一，次关五而税一，次关六而税一，并五关所税，适重一斤，问本持金几何”其意思为“今有人持金出五关，第1关收税金 $\frac{1}{2}$ ，第2关收税金为剩余金的 $\frac{1}{3}$ ，第3关收税金为剩余金的 $\frac{1}{4}$ ，第4关收税金为剩余金的 $\frac{1}{5}$ ，第5关收税金为剩余金的 $\frac{1}{6}$ ，5关所收税金之和，恰好重1斤，问原来持金多少？”若将题中“5关所收税金之和，恰好重1斤，问原来持金多少？”改成假设这个原来持金为x，按此规律通过第8关，则第8关需收税金为x．

查看试题解析
16. 在△ABC中，角A、B、C所对的边分别是a，b，c，cosC= $\frac{1}{9}$ ，且acosB+bcosA=2，则△ABC面积的最大值为．

查看试题解析

三、解答题

17. 在数列{a_n}和{b_n}中，a₁= $\frac{1}{2}$ ，{a_n}的前n项为S_n ，满足S_n₊₁+（ $\frac{1}{2}$ ）ⁿ⁺¹=S_n+（ $\frac{1}{2}$ ）ⁿ（n∈N^*），b_n=（2n+1）a_n ， {b_n}的前n项和为T_n ．

(1)、求数列{b_n}的通项公式b_n以及T_n ．

(2)、若T₁+T₃ ， mT₂ ， 3（T₂+T₃）成等差数列，求实数m的值．

查看试题解析
18. 如图，在三棱柱ABC﹣A₁B₁C₁中，侧面ACC₁A₁与侧面CBB₁C₁都是菱形，∠ACC₁=∠CC₁B₁=60°，AC=2 $\sqrt{3}$ ．

(1)、求证：AB₁⊥CC₁；

(2)、若AB₁=3 $\sqrt{2}$ ，A₁C₁的中点为D₁ ，求二面角C﹣AB₁﹣D₁的余弦值．

查看试题解析
19. 在高中学习过程中，同学们经常这样说：“如果物理成绩好，那么学习数学就没什么问题．”某班针对“高中生物理学习对数学学习的影响”进行研究，得到了学生的物理成绩与数学成绩具有线性相关关系的结论，现从该班随机抽取5名学生在一次考试中的物理和数学成绩，如表：
成绩/编号
1
2
3
4
5
物理（x）
90
85
74
68
63
数学（y）
130
125
110
95
90
（参考公式： $\hat{b}$ = $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a}$ = $\hat{y}$ ﹣ $\hat{b}$ $\bar{x}$ ）
参考数据：90²+85²+74²+68²+63²=29394，90×130+85×125+74×110+68×95+63×90=42595．

(1)、求数学成绩y关于物理成绩x的线性回归方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ （ $\hat{b}$ 精确到0.1），若某位学生的物理成绩为80分，预测他的数学成绩；

(2)、要从抽取的这五位学生中随机选出三位参加一项知识竞赛，以X表示选中的学生的数学成绩高于100分的人数，求随机变量X的分布列及数学期望．

查看试题解析
20. 设椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点分别为F₁、F₂ ，上顶点为A，过A与AF₂垂直的直线交x轴负半轴于Q点，且F₁恰好是线段QF₂的中点．

(1)、若过A、Q、F₂三点的圆恰好与直线3x﹣4y﹣7=0相切，求椭圆C的方程；

(2)、在（1）的条件下，B是椭圆C的左顶点，过点R（ $\frac{3}{2}$ ，0）作与x轴不重合的直线l交椭圆C于E、F两点，直线BE、BF分别交直线x= $\frac{8}{3}$ 于M、N两点，若直线MR、NR的斜率分别为k₁ ， k₂ ，试问：k₁k₂是否为定值？若是，求出该定值；若不是，请说明理由．

查看试题解析
21. 已知函数f（x）=2lnx﹣3x²﹣11x．

(1)、求曲线y=f（x）在点（1，f（1））处的切线方程；

(2)、若关于x的不等式f（x）≤（a﹣3）x²+（2a﹣13）x﹣2恒成，求整数a的最小值；

(3)、若正实数x₁ ， x₂满足f（x₁）+f（x₂）+4（x $_{1}^{2}$ +x $_{2}^{2}$ ）+12（x₁+x₂）=4，证明：x₁+x₂≥2．

查看试题解析
22. 以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的长度单位，已知直线l的参数方程为 ${\begin{matrix} x = t \sin ϕ \\ y = 2 + t \cos ϕ \end{matrix}$ （t为参数，0＜φ＜π），曲线C的极坐标方程为ρcos²θ=8sinθ．

(1)、求直线l的普通方程和曲线C的直角坐标方程；

(2)、设直线l与曲线C相交于A、B两点，当φ变化时，求|AB|的最小值．

查看试题解析
23. 已知函数f（x）=|x﹣2|．

(1)、求不等式f（x）+x²﹣4＞0的解集；

(2)、设g（x）=﹣|x+7|+3m，若关于x的不等式f（x）＜g（x）的解集非空，求实数m的取值范围．

查看试题解析

成绩/编号	1	2	3	4	5
物理（x）	90	85	74	68	63
数学（y）	130	125	110	95	90