2017年广东省深圳市高考数学一模试卷（理科）

试卷更新日期：2017-04-06 类型：高考模拟

进入出卷网下载

一、选择题：

1. 若集合A={2，4，6，8}，B={x|x²﹣9x+18≤0}，则A∩B=（）

A、{2，4} B、{4，6} C、{6，8} D、{2，8}

查看试题解析
2. 若复数 $\frac{a + i}{1 + 2 i}$ （a∈R）为纯虚数，其中i为虚数单位，则a=（）

A、2 B、3 C、﹣2 D、﹣3

查看试题解析
3. 袋中装有大小相同的四个球，四个球上分别标有数字“2”，“3”，“4”，“6”，现从中随机选取三个球，则所选的三个球上的数字能构成等差数列的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
4. 等比数列{a_n}的前n项和为S_n=a•3ⁿ^﹣¹+b，则 $\frac{a}{b}$ =（）

A、﹣3 B、﹣1 C、1 D、3

查看试题解析
5. 直线l：kx+y+4=0（k∈R）是圆C：x²+y²+4x﹣4y+6=0的一条对称轴，过点A（0，k）作斜率为1的直线m，则直线m被圆C所截得的弦长为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $\sqrt{6}$ D、2 $\sqrt{6}$

查看试题解析
6. 祖冲之之子祖暅是我国南北朝时代伟大的科学家，他在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”．意思是，如果两个等高的几何体在同高处截得的截面面积恒等，那么这两个几何体的体积相等．此即祖暅原理．利用这个原理求球的体积时，需要构造一个满足条件的几何体，已知该几何体三视图如图所示，用一个与该几何体的下底面平行相距为h（0＜h＜2）的平面截该几何体，则截面面积为（）

A、4π B、πh² C、π（2﹣h）² D、π（4﹣h）²

查看试题解析
7. 函数f（x）= $\frac{2^{x} + 1}{2^{x} - 1}$ •cosx的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 已知a＞b＞0，c＜0，下列不等关系中正确的是（）

A、ac＞bc B、a^c＞b^c C、log_a（a﹣c）＞log_b（b﹣c） D、 $\frac{a}{a - c}$ ＞ $\frac{b}{b - c}$

查看试题解析
9. 执行如图所示的程序框图，若输入p=2017，则输出i的值为（）

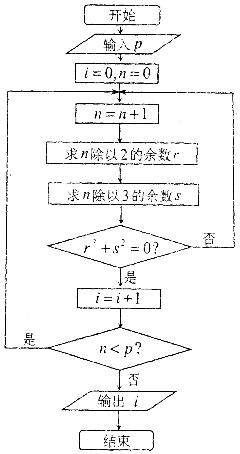A、335 B、336 C、337 D、338

查看试题解析
10. 已知F是双曲线E： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的右焦点，过点F作E的一条渐近线的垂线，垂足为P，线段PF与E相交于点Q，记点Q到E的两条渐近线的距离之积为d² ，若|FP|=2d，则该双曲线的离心率是（）

A、 $\sqrt{2}$ B、2 C、3 D、4

查看试题解析
11. 已知棱长为2的正方体ABCD﹣A₁B₁C₁D₁ ，球O与该正方体的各个面相切，则平面ACB₁截此球所得的截面的面积为（）

A、 $\frac{8 π}{3}$ B、 $\frac{5 π}{3}$ C、 $\frac{4 π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
12. 已知函数f（x）= $\frac{x^{2}}{e^{x}}$ ，x≠0，e为自然对数的底数，关于x的方程 $\sqrt{f (x)}$ + $\frac{2}{\sqrt{f (x)}}$ ﹣λ=0有四个相异实根，则实数λ的取值范围是（）

A、（0， $\frac{2}{e}$ ） B、（2 $\sqrt{2}$ ，+∞） C、（e+ $\frac{2}{e}$ ，+∞） D、（ $\frac{e^{2}}{2}$ + $\frac{4}{e^{2}}$ ，+∞）

查看试题解析

二、填空题：

13. 已知向量 $\vec{p}$ =（1，2）， $\vec{q}$ =（x，3），若 $\vec{p}$ ⊥ $\vec{q}$ ，则| $\vec{p}$ + $\vec{q}$ |= ．

查看试题解析
14. （ $\sqrt{x}$ ﹣ $\frac{1}{x}$ ）⁵的二项展开式中，含x的一次项的系数为（用数字作答）．

查看试题解析
15. 若实数x，y满足不等式组 ${\begin{matrix} x + y - 4 \leq 0 \\ 2 x - 3 y - 8 \leq 0 \\ x \geq 1 \end{matrix}$ ，目标函数z=kx﹣y的最大值为12，最小值为0，则实数k= ．

查看试题解析
16. 已知数列{a_n}满足na_n₊₂﹣（n+2）a_n=λ（n²+2n），其中a₁=1，a₂=2，若a_n＜a_n₊₁对∀n∈N^*恒成立，则实数λ的取值范围是．

查看试题解析

三、解答题：

17. △ABC的内角A、B、C的对边分别为a、b、c，已知2a= $\sqrt{3}$ csinA﹣acosC．

(1)、求C；

(2)、若c= $\sqrt{3}$ ，求△ABC的面积S的最大值．

查看试题解析
18. 如图，四边形ABCD为菱形，四边形ACEF为平行四边形，设BD与AC相交于点G，AB=BD=2，AE= $\sqrt{3}$ ，∠EAD=∠EAB．

(1)、证明：平面ACEF⊥平面ABCD；

(2)、若AE与平面ABCD所成角为60°，求二面角B﹣EF﹣D的余弦值．

查看试题解析
19. 某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按0.5元/度收费，超过200度但不超过400度的部分按0.8元/度收费，超过400度的部分按1.0元/度收费．

(1)、求某户居民用电费用y（单位：元）关于月用电量x（单位：度）的函数解析式；

(2)、为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电费用不超过260元的点80%，求a，b的值；

(3)、在满足（2）的条件下，若以这100户居民用电量的频率代替该月全市居民用户用电量的概率，且同组中的数据用该组区间的中点值代替，记Y为该居民用户1月份的用电费用，求Y的分布列和数学期望．

查看试题解析
20. 已成椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左右顶点分别为A₁、A₂ ，上下顶点分别为B₂/B₁ ，左右焦点分别为F₁、F₂ ，其中长轴长为4，且圆O：x²+y²= $\frac{12}{7}$ 为菱形A₁B₁A₂B₂的内切圆．

(1)、求椭圆C的方程；

(2)、点N（n，0）为x轴正半轴上一点，过点N作椭圆C的切线l，记右焦点F₂在l上的射影为H，若△F₁HN的面积不小于 $\frac{3}{16}$ n² ，求n的取值范围．

查看试题解析
21. 已知函数f（x）=xlnx，e为自然对数的底数．

(1)、求曲线y=f（x）在x=e^﹣²处的切线方程；

(2)、关于x的不等式f（x）≥λ（x﹣1）在（0，+∞）上恒成立，求实数λ的值；

(3)、关于x的方程f（x）=a有两个实根x₁ ， x₂ ，求证：|x₁﹣x₂|＜2a+1+e^﹣² ．

查看试题解析
22. 在直角坐标系中xOy中，已知曲线E经过点P（1， $\frac{2 \sqrt{3}}{3}$ ），其参数方程为 ${\begin{matrix} x = a \cos α \\ y = \sqrt{2} \sin α \end{matrix}$ （α为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系．

(1)、求曲线E的极坐标方程；

(2)、若直线l交E于点A、B，且OA⊥OB，求证： $\frac{1}{{| O A |}^{2}} + \frac{1}{{| O B |}^{2}}$ 为定值，并求出这个定值．

查看试题解析
23. 已知f（x）=|x+a|，g（x）=|x+3|﹣x，记关于x的不等式f（x）＜g（x）的解集为M．

(1)、若a﹣3∈M，求实数a的取值范围；

(2)、若[﹣1，1]⊆M，求实数a的取值范围．

查看试题解析