2017年甘肃省兰州市高考数学一模试卷(理科)
试卷更新日期:2017-04-06 类型:高考模拟
一、选择题
-
1. 已知集合M={x|(x﹣3)(x+1)≥0},N={x|﹣2≤x≤2},则M∩N=( )A、[﹣2,﹣1] B、[﹣1,2] C、[﹣1,1] D、[1,2]2. 已知复数z满足(3﹣4i)z=25,则z=( )A、﹣3﹣4i B、﹣3+4i C、3﹣4i D、3+4i3. 已知等差数列{an}的前n项和为Sn , 若a3+a5+a7=24,则S9=( )A、36 B、72 C、C144 D、2884. 已知某种商品的广告费支出x(单位;万元)与销售额y(单位:万元)之间有如下对应数据:
x
2
4
5
6
8
y
30
40
50
m
70
根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为 =6.5x+17.5,则表中m的值为( )
A、45 B、50 C、55 D、605. 下列命题中,真命题为( )A、∃x0∈R,e ≤0 B、∀x∈R,2x>x2 C、已知a,b为实数,则a+b=0的充要条件是 =﹣1 D、已知a,b为实数,则a>1,b>1是ab>1的充分不必要条件.6. 某几何体三视图如图所示,则该几何体的表面积为( )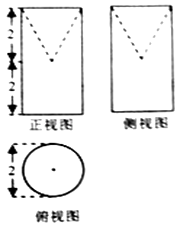 A、(9+ )π B、(9+2 )π C、(10+ )π D、(10+2 )π7. 设变量x,y满足不等式组 ,则x2+y2的最小值是( )A、 B、 C、 D、58. 如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的”更相减损术“.执行该程序框图,若输入a,b,i的值分别为6,8,0时,则输出的i=( )
A、(9+ )π B、(9+2 )π C、(10+ )π D、(10+2 )π7. 设变量x,y满足不等式组 ,则x2+y2的最小值是( )A、 B、 C、 D、58. 如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的”更相减损术“.执行该程序框图,若输入a,b,i的值分别为6,8,0时,则输出的i=( )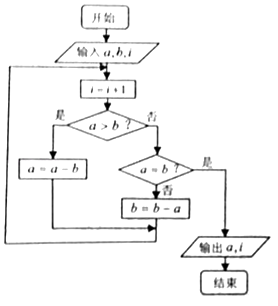 A、3 B、4 C、5 D、69. 已知圆C:(x﹣ )2+(y﹣1)2=1和两点A(﹣t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )A、( , ) B、( , ) C、( , ) D、( , )10. 函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|< )的部分图象如图所示,如果x1+x2= ,则f(x1)+f(x2)=( )
A、3 B、4 C、5 D、69. 已知圆C:(x﹣ )2+(y﹣1)2=1和两点A(﹣t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )A、( , ) B、( , ) C、( , ) D、( , )10. 函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|< )的部分图象如图所示,如果x1+x2= ,则f(x1)+f(x2)=( )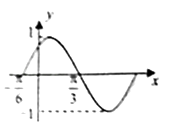 A、 B、 C、0 D、﹣11. 已知F1、F2为双曲线C: (a>0,b>0)的左、右焦点,点P为双曲线C右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则双曲线C的离心率为( )A、 B、 C、 D、212. 设函数f(x)在R上的导函数为f′(x),对∀x∈R有f(x)+f(﹣x)=x2 , 在(0,+∞)上f′(x)﹣x<0,若f(4﹣m)﹣f(m)≥8﹣4m,则实数m的取值范围是( )A、[2,+∞) B、(﹣∞,2] C、(﹣∞,2]∪[2,+∞) D、[﹣2,2]
A、 B、 C、0 D、﹣11. 已知F1、F2为双曲线C: (a>0,b>0)的左、右焦点,点P为双曲线C右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则双曲线C的离心率为( )A、 B、 C、 D、212. 设函数f(x)在R上的导函数为f′(x),对∀x∈R有f(x)+f(﹣x)=x2 , 在(0,+∞)上f′(x)﹣x<0,若f(4﹣m)﹣f(m)≥8﹣4m,则实数m的取值范围是( )A、[2,+∞) B、(﹣∞,2] C、(﹣∞,2]∪[2,+∞) D、[﹣2,2]二、填空题
-
13. cos2165°﹣sin215°= .14. 的展开式中,x2项的系数为 . (用数字作答)15. 已知在三棱锥P﹣ABC中,VP﹣ABC= ,∠APC= ,∠BPC= ,PA⊥AC,PB⊥BC,且平面PAC⊥平面PBC,那么三棱锥P﹣ABC外接球的体积为 .16. 已知数列{an}中,a1=1,Sn为数列{an}的前n项和,且当n≥2时,有 =1成立,则S2017= .
三、解答题
-
17. 已知在△ABC中,角A,B,C的对边分别为a,b,c,且asinB+bcosA=0.(1)、求角A的大小;(2)、若 ,求△ABC的面积.18. 随着人口老龄化的到来,我国的劳动力人口在不断减少,”延迟退休“已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄
[20,25)
[25,30)
[30,35)
[35,40)
[40,45)
人数
4
5
8
5
3
年龄
[45,50)
[50,55)
[55,60)
[60,65)
[65,70)
人数
6
7
3
5
4
经调查年龄在[25,30),[55,60)的被调查者中赞成人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为X,求随机变量X的分布列和数学期望.
19. 在正三棱柱ABC﹣A1B1C1中,AB=2,AA1=3,点D为BC的中点;(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)若点E为A1C上的点,且满足 =m (m∈R),若二面角E﹣AD﹣C的余弦值为 ,求实数m的值.
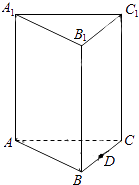 20. 已知椭圆C: =1(a>b>0)经过点( ,1),且离心率为 .
20. 已知椭圆C: =1(a>b>0)经过点( ,1),且离心率为 .(Ⅰ)求椭圆C的方程;
(Ⅱ)设M、N是椭圆C上的点,直线OM与ON(O为坐标原点)的斜率之积为﹣ ,若动点P满足 ,试探究,是否存在两个定点F1 , F2 , 使得|PF1|+|PF2|为定值?若存在,求F1 , F2的坐标,若不存在,请说明理由.