2017年安徽省宿州市灵璧县磬乡协作校中考数学一模试卷
试卷更新日期:2017-04-06 类型:中考模拟
一、选择题
-
1. ﹣4的倒数是( )A、﹣4 B、4 C、﹣ D、2. 若(x+2)(x﹣1)=x2+mx+n,则m+n=( )A、1 B、﹣2 C、﹣1 D、23. 我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( )
 A、5.5×106千米 B、5.5×107千米 C、55×106千米 D、0.55×108千米4. 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
A、5.5×106千米 B、5.5×107千米 C、55×106千米 D、0.55×108千米4. 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 分式方程 ﹣ =0的根是( )A、﹣1 B、1 C、3 D、06. 小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )A、5x+4(x+2)=44 B、5x+4(x﹣2)=44 C、9(x+2)=44 D、9(x+2)﹣4×2=447. 下列数据3,2,3,4,5,2,2的中位数是( )A、5 B、4 C、3 D、28. 如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )
5. 分式方程 ﹣ =0的根是( )A、﹣1 B、1 C、3 D、06. 小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )A、5x+4(x+2)=44 B、5x+4(x﹣2)=44 C、9(x+2)=44 D、9(x+2)﹣4×2=447. 下列数据3,2,3,4,5,2,2的中位数是( )A、5 B、4 C、3 D、28. 如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=52°,则∠EGF等于( )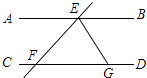 A、26° B、64° C、52° D、128°9.
A、26° B、64° C、52° D、128°9.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
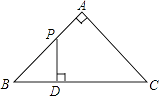 A、
A、 B、
B、 C、
C、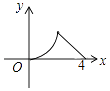 D、
D、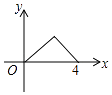 10. 如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣ 上,则使△ABC是直角三角形的点C的个数为( )
10. 如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣ 上,则使△ABC是直角三角形的点C的个数为( )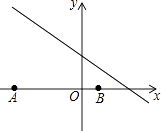 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 不等式组 的解集是 .12. 分解因式:x3﹣2x2+x= .13. 如图,正十二边形A1A2…A12 , 连接A3A7 , A7A10 , 则∠A3A7A10= .
 14.
14.如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是 .

三、解答题
-
15. 计算:|﹣3|+ tan30°﹣ ﹣(2017﹣π)0 .16. 先化简,再求值:( ﹣x﹣1)÷ ,选一个你喜欢的数代入求值.
四、解答题
-
17. 如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(﹣3,1),B(0,3),C(0,1)
 (1)、将△ABC以点O为旋转中心顺时针旋转90°,画出旋转后对应的△A1B1C1;(2)、分别连结AB1 , BA1后,求四边形ABA1B1的面积.18. 观察下列关于自然数的等式:
(1)、将△ABC以点O为旋转中心顺时针旋转90°,画出旋转后对应的△A1B1C1;(2)、分别连结AB1 , BA1后,求四边形ABA1B1的面积.18. 观察下列关于自然数的等式:(i)32﹣4×12=5 ①
(ii)52﹣4×22=9 ②
(iii)72﹣4×32=13 ③
…
根据上述规律解决下列问题:
(1)、完成第五个等式:112﹣4× 2=;(2)、写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.五、解答题
-
19.
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+ )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
 20. 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
20. 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6. (1)、求一次函数与反比例函数的解析式;(2)、求两函数图象的另一个交点坐标;(3)、直接写出不等式;kx+b≤ 的解集.
(1)、求一次函数与反比例函数的解析式;(2)、求两函数图象的另一个交点坐标;(3)、直接写出不等式;kx+b≤ 的解集.六、解答题
-
21. 某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号
分组
频数
一
6≤m<7
2
二
7≤m<8
7
三
8≤m<9
a
四
9≤m≤10
2
(1)、求a的值;(2)、若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;(3)、将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).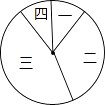
七、解答题
-
22. 如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
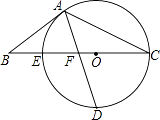 (1)、求证:AB是⊙O的切线;(2)、若CF=4,DF= ,求⊙O的半径r及sinB.
(1)、求证:AB是⊙O的切线;(2)、若CF=4,DF= ,求⊙O的半径r及sinB.八、解答题
-
23.
如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
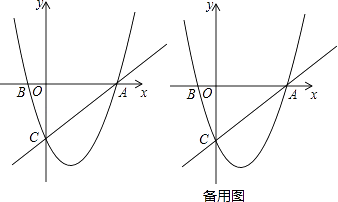 (1)、b= , c= , 点B的坐标为;(直接填写结果)(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
(1)、b= , c= , 点B的坐标为;(直接填写结果)(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
-
-