2017年浙江省数学中考模拟卷(一)
试卷更新日期:2017-04-06 类型:中考模拟
一、选择题。
-
1. 一粒芝麻约有0.000002千克,0.000002用科学记数学法表示为( )千克.A、2×10﹣4 B、0.2×10﹣5 C、2×10﹣7 D、2×10﹣62. 随着我国经济快速发展,轿车进入百姓家庭,小明同学在街头观察出下列四种汽车标志,其中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 (a4)3=a7 B、 3﹣2=﹣32 C、 (2ab)3=6a3b3 D、 ﹣a5•a5=﹣a104. 若关于x的一元二次方程x2﹣2x﹣k+1=0有两个不相等的实数根,则一次函数y=kx﹣k的大致图象是( )A、
3. 下列计算正确的是( )A、 (a4)3=a7 B、 3﹣2=﹣32 C、 (2ab)3=6a3b3 D、 ﹣a5•a5=﹣a104. 若关于x的一元二次方程x2﹣2x﹣k+1=0有两个不相等的实数根,则一次函数y=kx﹣k的大致图象是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
5. 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )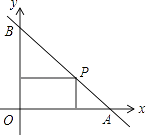 A、y=x+5 B、y=x+10 C、y=﹣x+5 D、y=﹣x+106. 下列命题中,真命题的个数是( )
A、y=x+5 B、y=x+10 C、y=﹣x+5 D、y=﹣x+106. 下列命题中,真命题的个数是( )①同位角相等
②经过一点有且只有一条直线与这条直线平行
③长度相等的弧是等弧
④顺次连接菱形各边中点得到的四边形是矩形.
A、1个 B、2个 C、3个 D、4个7. 在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17.2,则四个班体考成绩最稳定的是( )A、甲班 B、乙班 C、丙班 D、丁班8. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )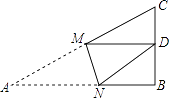 A、 B、 C、4 D、59.
A、 B、 C、4 D、59.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
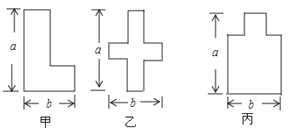 A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝一样长10.
A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝一样长10.梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过10千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( ).
 A、1个 B、2个 C、3个 D、4个11. 在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文的26个字母a、b、c,…,z依次对应1、2、3,…,26这26个自然数(见表格),当明码对应的序号x为奇数时,密码对应的序号y=;当明码对应的序号x为偶数时,密码对应的序号y= .
A、1个 B、2个 C、3个 D、4个11. 在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文的26个字母a、b、c,…,z依次对应1、2、3,…,26这26个自然数(见表格),当明码对应的序号x为奇数时,密码对应的序号y=;当明码对应的序号x为偶数时,密码对应的序号y= .字母
a
b
c
d
e
f
g
h
i
j
k
l
m
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
14
15
16
17
18
19
20
21
22
23
24
25
26
按上述规定,将明码“bird”译成密码是( )
A、bird B、nove C、sdri D、nevo12. 已知函数 ,则下列函数图象正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题。
-
13. ﹣1 的相反数是 , 倒数是 .14. 若x<2,化简 +|3﹣x|的正确结果是 .15. 某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有人.
每周课外阅读时间(小时)
0~1
1~2(不含1)
2~3(不含2)
超过3
人 数
7
10
14
19
16. 已知在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .17. 如图,正方形ABCD的边长为1,分别以A.D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积 18.
18.如图,在▱ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处.若△FDE的周长为5,△FCB的周长为17,则FC的长为 .

三、解答题。
-
19. 计算:20. 先化简 ,然后选择一个你喜欢的数代入求值.21. 某人的钱包内有10元钱、20元钱和50元钱的纸币各1张,从中随机取出2张纸币.(1)、求取出纸币的总额是30元的概率;(2)、求取出纸币的总额可购买一件51元的商品的概率.22. 小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图,A,B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=140cm,小梅的连衣裙穿在衣架后的总长度为122cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
 23. 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
23. 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(1)、求证:△ADE≌△ABF.(2)、求△AEF的面积.
24. 观察下表:序号
1
2
3
…
图形
x x
y
x x
x x x
y y
x x x
y y
x x x
x x x x
y y y
x x x x
y y y
x x x x
y y y
x x x x
…
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)、第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;(2)、若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.①求x,y的值;
②在此条件下,第n个特征多项式是否有最小值?若有,求出最小值和相应的n值.若没有,请说明理由.
25. 如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)、求线段CD的长;(2)、如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(3)、如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
26. 如图,抛物线 y=ax2+bx+c(a≠0)经过点A(-3,0)、B(1,0)、C(-2,1),交y轴于点M.
(1)、求抛物线的表达式;(2)、D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;(3)、抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A.N为顶点的三角形与△MAO相似?若存在,求点P的坐标;若不存在,请说明理由.