浙江省温州市鹿城区2018届数学中考模拟试卷
试卷更新日期:2018-12-28 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、
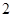 B、
C、
D、
2. 由五个小立方体搭成的几何体如图所示,其主视图是
B、
C、
D、
2. 由五个小立方体搭成的几何体如图所示,其主视图是 A、
A、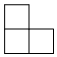 B、
B、 C、
C、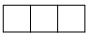 D、
D、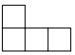 3. 事件:“在只装有2个红球和8个黑球的袋子里,摸出一个白球”是 )A、可能事件 B、随机事件 C、不可能事件 D、必然事件4. 不等式 的解是A、
3. 事件:“在只装有2个红球和8个黑球的袋子里,摸出一个白球”是 )A、可能事件 B、随机事件 C、不可能事件 D、必然事件4. 不等式 的解是A、 B、
B、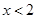 C、
D、
5. 在一次中学生田径运动会上,参加男子跳高的20名运动员的成绩如下表所示:
C、
D、
5. 在一次中学生田径运动会上,参加男子跳高的20名运动员的成绩如下表所示:成绩 米
人数
4
3
5
6
1
1
则这些运动员成绩的众数为
A、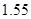 米
B、
米
B、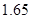 米
C、
米
C、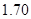 米
D、
米
D、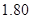 米
6. 已知点 , 在一次函数 的图象上,则 , ,0的大小关系是A、
米
6. 已知点 , 在一次函数 的图象上,则 , ,0的大小关系是A、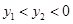 B、
B、 C、
C、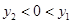 D、
D、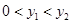 7. 如图,一架长 米的梯子AB斜靠在墙上,已知梯子底端B到墙角C的距离为 米,设梯子与地面所夹的锐角为 ,则 的值为
7. 如图,一架长 米的梯子AB斜靠在墙上,已知梯子底端B到墙角C的距离为 米,设梯子与地面所夹的锐角为 ,则 的值为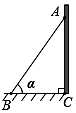 A、 B、 C、 D、8. 我们知道方程组 的解是 ,现给出另一个方程组 ,它的解是A、
A、 B、 C、 D、8. 我们知道方程组 的解是 ,现给出另一个方程组 ,它的解是A、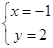 B、
B、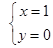 C、
C、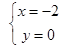 D、
D、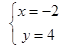 9. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板” 如图是一个七巧板迷宫,它恰好拼成了一个正方形ABCD,其中E,P分别是AD,CD的中点,一只蚂蚁从点A处沿图中实线爬行到出口点P处 若 ,则它爬行的最短路程为
9. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板” 如图是一个七巧板迷宫,它恰好拼成了一个正方形ABCD,其中E,P分别是AD,CD的中点,一只蚂蚁从点A处沿图中实线爬行到出口点P处 若 ,则它爬行的最短路程为 A、 B、 C、 D、310. 如图,在▱ABCD中, , , 分别切边AB,AD于点E,F,且圆心O恰好落在DE上 现将 沿AB方向滚动到与边BC相切 点O在 的内部 ,则圆心O移动的路径长为
A、 B、 C、 D、310. 如图,在▱ABCD中, , , 分别切边AB,AD于点E,F,且圆心O恰好落在DE上 现将 沿AB方向滚动到与边BC相切 点O在 的内部 ,则圆心O移动的路径长为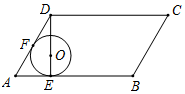 A、4 B、6 C、
A、4 B、6 C、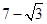 D、
D、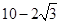
二、填空题
-
11. 分解因式:m2+2m= .12. 小红同学5月份各项消费情况的扇形统计图如图所示,其中小红在学习用品上支出100元,则在午餐上支出元
 13. 如图,在 中, ,则 度.
13. 如图,在 中, ,则 度.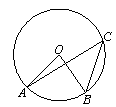 14. 甲、乙两工程队分别承接了250米、150米的道路铺设任务,已知乙比甲每天多铺设5米,甲完成铺设任务的时间是乙的2倍 设甲每天铺设x米,则根据题意可列出方程: .15. 如图,点A在第一象限,作 轴,垂足为点B,反比例函数 的图象经过AB的中点C,过点A作 轴,交该函数图象于点 是AC的中点,连结OE,将 沿直线OE对折到 ,使 恰好经过点D,若 ,则k的值是 .
14. 甲、乙两工程队分别承接了250米、150米的道路铺设任务,已知乙比甲每天多铺设5米,甲完成铺设任务的时间是乙的2倍 设甲每天铺设x米,则根据题意可列出方程: .15. 如图,点A在第一象限,作 轴,垂足为点B,反比例函数 的图象经过AB的中点C,过点A作 轴,交该函数图象于点 是AC的中点,连结OE,将 沿直线OE对折到 ,使 恰好经过点D,若 ,则k的值是 .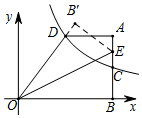 16. 如图,矩形ABCD和正方形EFGH的中心重合, , , 分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K, 若 ,则AI的长为 , 四边形AIEL的面积为 .
16. 如图,矩形ABCD和正方形EFGH的中心重合, , , 分别延长FE,GF,HG和EH交AB,BC,CD,AD于点I,J,K, 若 ,则AI的长为 , 四边形AIEL的面积为 .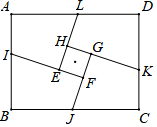
三、解答题
-
17.(1)、计算: .(2)、化简: .18. 如图,在 中, ,CD是 的平分线, ,交AC于点E.
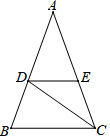 (1)、求证: .(2)、若 ,求 的度数.19. 电视节目“奔跑吧兄弟”播出后深受中学生喜爱,小睿想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取部分学生进行抽查 每人只能选一个自己最喜欢的“兄弟” ,得到如图所示的统计图,
(1)、求证: .(2)、若 ,求 的度数.19. 电视节目“奔跑吧兄弟”播出后深受中学生喜爱,小睿想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取部分学生进行抽查 每人只能选一个自己最喜欢的“兄弟” ,得到如图所示的统计图,请结合图中提供的信息解答下列问题:
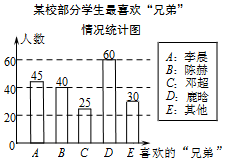 (1)、若小睿所在学校有1800名学生,估计全校喜欢“鹿晗”兄弟的学生人数.(2)、小睿和小轩都喜欢“陈赫”,小彤喜欢“鹿晗”,从他们三人中随机抽选两人参加“撕名牌”游戏,求选中的两人中“一人喜欢陈赫,一人喜欢鹿晗”的概率 要求列表或画树状图(3)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(4)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.20. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形 如图,已知整点 , ,请在所给网格上按要求画整点四边形.
(1)、若小睿所在学校有1800名学生,估计全校喜欢“鹿晗”兄弟的学生人数.(2)、小睿和小轩都喜欢“陈赫”,小彤喜欢“鹿晗”,从他们三人中随机抽选两人参加“撕名牌”游戏,求选中的两人中“一人喜欢陈赫,一人喜欢鹿晗”的概率 要求列表或画树状图(3)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(4)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.20. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形 如图,已知整点 , ,请在所给网格上按要求画整点四边形. (1)、若小睿所在学校有1800名学生,估计全校喜欢“鹿晗”兄弟的学生人数.(2)、小睿和小轩都喜欢“陈赫”,小彤喜欢“鹿晗”,从他们三人中随机抽选两人参加“撕名牌”游戏,求选中的两人中“一人喜欢陈赫,一人喜欢鹿晗”的概率 要求列表或画树状图(3)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(4)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.21. 如图,在 中, ,E是边BC上一点,以AE为直径的 经过点C,并交AB于点D,连结ED.
(1)、若小睿所在学校有1800名学生,估计全校喜欢“鹿晗”兄弟的学生人数.(2)、小睿和小轩都喜欢“陈赫”,小彤喜欢“鹿晗”,从他们三人中随机抽选两人参加“撕名牌”游戏,求选中的两人中“一人喜欢陈赫,一人喜欢鹿晗”的概率 要求列表或画树状图(3)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(4)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.21. 如图,在 中, ,E是边BC上一点,以AE为直径的 经过点C,并交AB于点D,连结ED.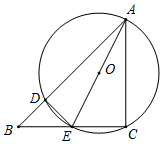 (1)、判断 的形状并证明.(2)、连结CO并延长交AB于点F,若 ,求AF的长.22. 如图,在平面直角坐标系中,抛物线 交x轴正半轴于点A,M是抛物线对称轴上的一点, ,过点M作x轴的平行线交抛物线于点B, 在C的左边 ,交y轴于点D,连结OB,OC.
(1)、判断 的形状并证明.(2)、连结CO并延长交AB于点F,若 ,求AF的长.22. 如图,在平面直角坐标系中,抛物线 交x轴正半轴于点A,M是抛物线对称轴上的一点, ,过点M作x轴的平行线交抛物线于点B, 在C的左边 ,交y轴于点D,连结OB,OC.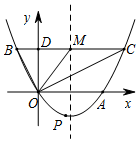 (1)、求OA,OD的长.(2)、求证: .(3)、P是抛物线上一点,当 时,求点P的坐标.23. 某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)、求OA,OD的长.(2)、求证: .(3)、P是抛物线上一点,当 时,求点P的坐标.23. 某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.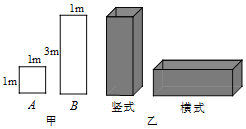 (1)、若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?(2)、若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?(3)、若该工厂新购得65张规格为 的C型正方形板材,将其全部切割成A型或B型板材 不计损耗 ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共只24. 如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连结BD,设AP=m.
(1)、若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?(2)、若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?(3)、若该工厂新购得65张规格为 的C型正方形板材,将其全部切割成A型或B型板材 不计损耗 ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共只24. 如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连结BD,设AP=m.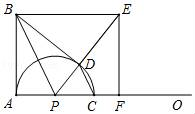 (1)、求证:∠BDP=90°.(2)、若m=4,求BE的长.(3)、在点P的整个运动过程中.
(1)、求证:∠BDP=90°.(2)、若m=4,求BE的长.(3)、在点P的整个运动过程中.①当AF=3CF时,求出所有符合条件的m的值.
②当tan∠DBE= 时,直接写出△CDP与△BDP面积比.