浙江省杭州市上城区2018届数学中考一模试卷
试卷更新日期:2018-12-28 类型:中考模拟
一、单选题
-
1. -5的相反数是( )A、5 B、
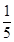 C、
D、
C、
D、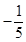 2. 浙江省陆域面积为101800平方千米。数据101800用科学记数法表示为( )A、1.018×104 B、1.018×105 C、10.18×105 D、0.1018×1063. 下列运算正确的是( )
2. 浙江省陆域面积为101800平方千米。数据101800用科学记数法表示为( )A、1.018×104 B、1.018×105 C、10.18×105 D、0.1018×1063. 下列运算正确的是( )
A、(a4)3=a7 B、a6÷a3=a2 C、(2ab)3=6a3b3 D、﹣a5•a5=﹣a104. 四张分别画有平行四边形、菱形、等边三角形、圆的卡片,它们的背面都相同。现将它们背面朝上,从中任取一张,卡片上所画图形恰好是中心对称图形的概率是( )A、 B、1 C、 D、5. 若代数式 , ,则M与N的大小关系是( )A、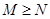 B、
B、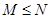 C、
C、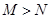 D、
D、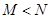 6. 下表是某校合唱团成员的年龄分布,对于不同的x,下列关于年龄的统计量不会发生改变的是( )
6. 下表是某校合唱团成员的年龄分布,对于不同的x,下列关于年龄的统计量不会发生改变的是( )年龄/岁
13
14
15
16
频数
5
15
x
10- x
A、平均数、中位数 B、众数、方差 C、平均数、方差 D、众数、中位数7. 如图,⊙O的半径OC与弦AB交于点D,连结OA,AC,CB,BO,则下列条件中,无法判断四边形OACB为菱形的是( )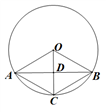 A、∠DAC=∠DBC=30° B、OA∥BC,OB∥AC B. C、AB与OC互相垂直 D、AB与OC互相平分8. 已知∠BAC=45。 , 一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是( )A、0<x≤1 B、 1≤x<
A、∠DAC=∠DBC=30° B、OA∥BC,OB∥AC B. C、AB与OC互相垂直 D、AB与OC互相平分8. 已知∠BAC=45。 , 一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是( )A、0<x≤1 B、 1≤x<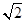 C、 0<x≤
C、 0<x≤ 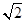 D、 x>
D、 x> 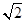 9. 已知关于x的不等式ax<b的解为x>-2,则下列关于x的不等式中,解为x<2的是( )A、ax+2<-b+2 B、–ax-1<b-1 C、ax>b D、
9. 已知关于x的不等式ax<b的解为x>-2,则下列关于x的不等式中,解为x<2的是( )A、ax+2<-b+2 B、–ax-1<b-1 C、ax>b D、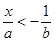 10. 对于代数式ax2+bx+c(a≠0),下列说法正确的是( )
10. 对于代数式ax2+bx+c(a≠0),下列说法正确的是( )①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则a +bx+c=a(x-p)(x-q)②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
A、③ B、①③ C、②④ D、①③④二、填空题
-
11. 分解因式:a3-4a= .
12. 已知 x(x+1)=x+1,则x=.13. 在Rt△ABC中,∠C=90∘,若AB=4,sinA = ,则斜边AB边上的高CD的长为.14. 已知一块等腰三角形钢板的底边长为60cm,腰长为50 cm,能从这块钢板上截得得最大圆得半径为cm15. 已知函数y= -1,给出一下结论:①y的值随x的增大而减小②此函数的图形与x轴的交点为(1,0)③当x>0时,y的值随x的增大而越来越接近-1④当x≤ 时,y的取值范围是y≥1以上结论正确的是(填序号)
16. 已知图中Rt△ABC,∠B=90°,AB=BC,斜边AC上的一点D,满足AD=AB,将线段AC绕点A逆时针旋转α (0°<α <360°),得到线段ac’,连接dc’,当dc’ bc时,旋转角度α 的值为 ,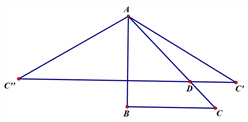
三、解答题
-
17. 某校对学生就“食品安全知识”进行了抽样调查(每人选填一类),绘制了如图所示的两幅统计图(不完整)。请根据图中信息,解答下列问题:
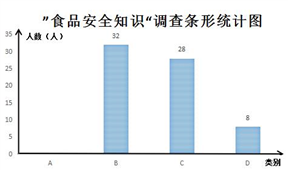
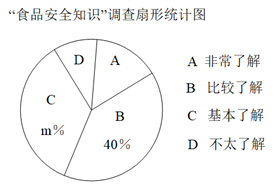 (1)、根据图中数据,求出扇形统计图中 的值,并补全条形统计图。(2)、该校共有学生900人,估计该校学生对“食品安全知识”非常了解的人数.18. 在平面直角坐标系中,关于 的一次函数的图象经过点 ,且平行于直线 .(1)、求该一次函数表达式;(2)、若点Q(x,y)是该一次函数图象上的点,且点Q在直线 的下方,求x的取值范围.19. 已知线段a及如图形状的图案.
(1)、根据图中数据,求出扇形统计图中 的值,并补全条形统计图。(2)、该校共有学生900人,估计该校学生对“食品安全知识”非常了解的人数.18. 在平面直角坐标系中,关于 的一次函数的图象经过点 ,且平行于直线 .(1)、求该一次函数表达式;(2)、若点Q(x,y)是该一次函数图象上的点,且点Q在直线 的下方,求x的取值范围.19. 已知线段a及如图形状的图案.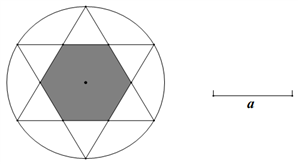 (1)、用直尺和圆规作出图中的图案,要求所作图案中圆的半径为a(保留作图痕迹)(2)、当a=6时,求图案中阴影部分正六边形的面积.20. 为节约用水,某市居民生活用水按阶梯式水价计量,水价分为三个阶梯,价格表如下表所示:
(1)、用直尺和圆规作出图中的图案,要求所作图案中圆的半径为a(保留作图痕迹)(2)、当a=6时,求图案中阴影部分正六边形的面积.20. 为节约用水,某市居民生活用水按阶梯式水价计量,水价分为三个阶梯,价格表如下表所示:某市自来水销售价格表
类别
月用水量
(立方米)
供水价格
(元/立方米)
污水处理费
(元/立方米)
居民生活用水
阶梯一
0~18(含18)
1.90
1.00
阶梯二
18~25(含25)
2.85
阶梯三
25以上
5.70
(注:居民生活用水水价=供水价格+污水处理费)
(1)、当居民月用水量在18立方米及以下时,水价是元/立方米.(2)、4月份小明家用水量为20立方米,应付水费为:18×(1.90+1.00)+2×(2.85+1.00)=59.90(元)
预计6月份小明家的用水量将达到30立方米,请计算小明家6月份的水费.
(3)、为了节省开支,小明家决定每月用水的费用不超过家庭收入的1%,已知小明家的平均月收入为7530元,请你为小明家每月用水量提出建议21. 如图,已知□ABCD的面积为S,点P、Q时是▱ABCD对角线BD的三等分点,延长AQ、AP,分别交BC,CD于点E,F,连结EF。甲,乙两位同学对条件进行分析后,甲得到结论①:“E是BC中点” .乙得到结论②:“四边形QEFP的面积为 S”。请判断甲乙两位同学的结论是否正确,并说明理由.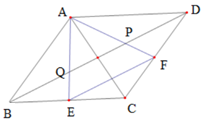 22. 已知 关于 的二次函数(1)、当 时,求该函数图象的顶点坐标.(2)、在(1)条件下, 为该函数图象上的一点,若 关于原点的对称点 也落在该函数图象上,求 的值(3)、当函数的图象经过点(1,0)时,若 是该函数图象上的两点,试比较 与 的大小.23. 如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.
22. 已知 关于 的二次函数(1)、当 时,求该函数图象的顶点坐标.(2)、在(1)条件下, 为该函数图象上的一点,若 关于原点的对称点 也落在该函数图象上,求 的值(3)、当函数的图象经过点(1,0)时,若 是该函数图象上的两点,试比较 与 的大小.23. 如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.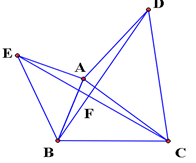 (1)、求证:∠BDA=∠ECA.(2)、若m= ,n=3,∠ABC=75°,求BD的长.(3)、当∠ABC=时,BD最大,最大值为(用含m,n的代数式表示)(4)、试探究线段BF,AE,EF三者之间的数量关系。
(1)、求证:∠BDA=∠ECA.(2)、若m= ,n=3,∠ABC=75°,求BD的长.(3)、当∠ABC=时,BD最大,最大值为(用含m,n的代数式表示)(4)、试探究线段BF,AE,EF三者之间的数量关系。