云南省昆明市西山区2018届数学中考二模试卷
试卷更新日期：2018-12-28 类型：中考模拟
一、单选题
-
1. 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（ ）A、
B、
C、
D、
2. 我国对“一带一路”沿线国家不断加大投资，目前已为有关国家创造了近1100000000美元税收，其中1100000000用科学记数法表示应为（ ）A、0.11×108 B、1.1×109 C、1.1×1010 D、11×1083. 下列计算正确的是（ ）A、2x+3y=5xy B、(m+3)2=m2+9 C、(xy2)3=xy6 D、a10÷a5=a54. 函数y= 中，自变量x的取值范围是（ ）A、x＞﹣3 B、x≥﹣3 C、x≠﹣3 D、x≤﹣35. 下列说法中，正确的说法有（ ）①对角线互相平分且相等的四边形是菱形；②一元二次方程x2﹣3x﹣4=0的根是x1=4，x2=﹣1；③依次连接任意一个四边形各边中点所得的四边形是平行四边形；④一元一次不等式2x+5＜11的正整数解有3个；⑤八边形内角和是外角和的4倍．
A、1个 B、2个 C、3个 D、4个6.如图，在⊙O的内接四边形ABCD中，∠BOD=120°，那么∠BCD是（ ）
A、120° B、100° C、80° D、60°7. 如图，四边形QABC是矩形，ADEF是正方形，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y=的图象上，OA=1，OC=6，则正方形ADEF的边长为（ ）
A、2 B、3 C、4 D、5二、填空题
-
8. 如果向东走18米记为+18，那么向西走18米记为 ．9. 如图，直线a∥b，c与直线a、b分别相交于A、B两点，若∠1=50度，则∠2=度．
10. 阅读理解：引入新数i，新数i满足分配律，结合律，交换律，已知i2=﹣1，那么（1+i）•（1﹣i）= ．11. 一组数据4，5，a，7，9的平均数是6，则这组数据的中位数是 ．12. 已知：如图，圆锥的底面直径是10cm，高为12cm，则它的表面积是cm2 ．
13. 如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，那么线段EF的长为 ．
三、解答题
-
14.(1)、计算：（ ﹣1）0﹣（﹣ ）﹣2+ tan30°．(2)、解方程 ．15. 先化简．再求值（ ）÷ ，其中x满足x2﹣x﹣1=0．16. 如图，点E，F在AB上，AD=BC，∠A=∠B，AE=BF．求证：∠C=∠D．
17. 某校为了解九年级男同学的体育考试准备情况，随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
(1)、根据给出的信息，补全两幅统计图；(2)、该校九年级有600名男生，请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛，预赛分为A、B、C三组进行，选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?18. 如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在OA的位置时俯角∠EOA=30°，在OB的位置时俯角∠FOB=60°，若OC⊥EF，点A比点B高7cm，求单摆的长度（结果精确到0.1，参考数据： ≈ 1.73）．
19. 某中学为打造书香校园，计划购进甲、乙两种规格的书柜放置新购进的图书，调查发现，若购买甲种书柜3个、乙种书柜2个，共需资金1020元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元．
(1)、甲、乙两种书柜每个的价格分别是多少元？
(2)、若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，学校至多能够提供资金4320元，请设计几种购买方案供这个学校选择．
20. 如图，已知四边形ABCD为矩形，AD=20cm、AB=10cm．M点从D到A，P点从B到C，两点的速度都为2cm/s；N点从A到B，Q点从C到D，两点的速度都为1cm/s．若四个点同时出发．
(1)、判断四边形MNPQ的形状．(2)、四边形MNPQ能为菱形吗？若能，请求出此时运动的时间；若不能，说明理由．21. 定义：如图1，抛物线y=ax2+bx+c（a≠0）与x轴交于A，B两点，点P在该抛物线上（P点与A、B两点不重合），如果△ABP的三边满足AP2+BP2=AB2 ， 则称点P为抛物线y=ax2+bx+c（a≠0）的勾股点．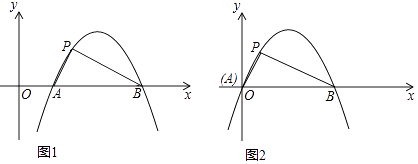
(1)、直接写出抛物线y=﹣x2+1的勾股点的坐标．(2)、如图2，已知抛物线C：y=ax2+bx（a≠0）与x轴交于A，B两点，点P（1， ）是抛物线C的勾股点，求抛物线C的函数表达式．
(3)、在（2）的条件下，点Q在抛物线C上，求满足条件S△ABQ=S△ABP的Q点（异于点P）的坐标．