云南省昆明市五华区2018届数学中考一模试卷

试卷更新日期：2018-12-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 据国土资源部数据显示，我国是全球“可燃冰”资源储量最多的国家之一，海、陆总储量约为39000000000吨油当量，将39000000000用科学记数法表示为 $($ $)$

A、 B、 C、 D、

查看试题解析
2. 我国古代数学家利用“牟合方盖”（如图甲）找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体．图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是 $($ $)$

A、 B、 C、 D、

查看试题解析
4. 李老师为了了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体情况统计如下：
阅读时间
（小时）
2
2.5
3
3.5
4
学生人数（名）
1
2
8
6
3
则关于这20名学生阅读小时数的说法正确的是（）

A、众数是8 B、中位数是3 C、平均数是3 D、方差是0.34

查看试题解析
5. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x的值为 $($ $)$

A、 $- 2$ B、0 C、2 D、 $\pm 2$

查看试题解析
6. 求证：菱形的两条对角线互相垂直．
已知：如图所示，四边形ABCD是菱形，对角线AC，BD交于点O．

求证： $AC ⊥ BD$ ．

以下是打乱的证明过程： $① ∵ BO = DO$ ， $② ∴ AO$ 是BD的垂直平分线，即 $AC ⊥ BD$ ． $③ ∵$ 四边形ABCD是菱形， $④ ∴ AB = AD$ ．证明步骤正确的顺序是（）

A、 B、 C、 D、

查看试题解析
7. 下列方程中，没有实数根的是 $($ $)$

A、 B、 C、 D、

查看试题解析
8. 如图所示，正方形ABCD中，BE=EF=FC，CG=2GD，BG分别交AE，AF于M，N，下列结论：①AF⊥BG；②BN= $\frac{4}{3}$ NF；③ $\frac{B M}{M G} = \frac{3}{8}$ ；④S_{四边形CGNF}= $\frac{1}{2}$ S_{四边形ANGD} ．其中正确的结论的序号是（）

A、①③ B、②④ C、①② D、③④

查看试题解析

二、填空题

9. $\frac{1}{6}$ 的倒数是．

查看试题解析
10. 如图，小敏做了一个角平分仪ABCD，其中 $AB = AD$ ， $BC = DC$ ，将仪器上的点A与 $∠ PRQ$ 的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是 $∠ PRQ$ 的平分线 $.$ 此角平分仪的画图原理是：根据仪器结构，可得 $△ ABC$ ≌ $△ ADC$ ，这样就有 $∠ QAE = ∠ PAE .$ 则说明这两个三角形全等的依据是

查看试题解析
11. 下列分式化简运算中，每一步运算都在后面列出了依据，所列依据错误的是 $($ 只填写序号 $)$
计算： $\frac{3 a}{a + b} + \frac{a + 4 b}{a + b}$

解：原式 $= \frac{3 a + a + 4 b}{a + b} ①$ 同分母分式的加减法法则

$= \frac{4 a + 4 b}{a + b} ②$ 合并同类项法则

$= \frac{4 (a + b)}{a + b} ③$ 提公因式法

$= 4 ④$ 等式的基本性质

查看试题解析
12. 一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是．

查看试题解析
13. 端午节前夕，某超市用1680元购进A，B两种商品共60件，其中A种商品每件24元，B种商品每件36元，设购买A种商品x件，B种商品y件，依题意列出的方程组是．

查看试题解析
14. “赶陀螺”是一项深受人们喜爱的运动，如图所示是一个陀螺的立体结构图，已知底面圆的直径 $AB = 8 cm$ ，圆柱体部分的高 $BC = 6 cm$ ，圆锥体部分的高 $CD = 3 cm$ ，则这个陀螺的表面积是 ${cm}^{2}$ ．

查看试题解析

三、解答题

15.

(1)、计算： $| 2 - \sqrt{3} | + {(\frac{1}{3})}^{- 1} - {(3 - π)}^{0} - {(- 1)}^{2019}$ ．

(2)、解不等式组： ${\begin{matrix} 2 x - 3 > 1 \\ \frac{2 - x}{3} > \frac{x}{3} - 2 \end{matrix}$

查看试题解析
16. 某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况，随机抽查部分学生做了一次问卷调查，要求学生选出自己最喜欢的一个版面，将调查数据进行了整理、绘制成部分统计图如下：

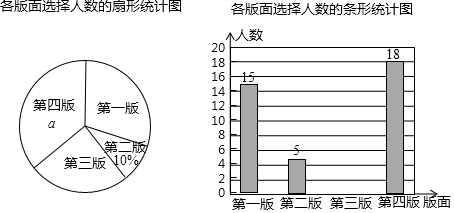
请根据图中信息，解答下列问题：

(1)、该调查的样本容量为， $a =$ $%$ ，“第一版”对应扇形的圆心角为 $^{\circ}$ ；

(2)、请你补全条形统计图；

(3)、若该校有1000名学生，请你估计全校学生中最喜欢“第三版”的人数．

查看试题解析
17. 为了弘扬优秀传统文化，某校组织了一次“诗词大会”，小明和小丽同时参加，其中，有一道必答题是：从如图所示的九宫格中选取七个字组成一句唐诗，其答案为“两个黄鹂鸣翠柳”．

(1)、小明回答该问题时，对第二个字是选“个”还是选“只”难以抉择，若随机选择其中一个，则小明回答正确的概率是；

(2)、小丽回答该问题时，对第二个字是选“个”还是选“只”、第五个字是选“鸣”还是选“明”都难以抉择，若分别随机选择，请用列表或画树状图的方法求小丽回答正确的概率．

查看试题解析
18. 如图，一枚运载火箭从距雷达站C处5km的地面O处发射，当火箭到达点A，B时，在雷达站C处测得点A，B的仰角分别为 $34^{\circ}$ ， $45^{\circ}$ ，其中点O，A，B在同一条直线上 $.$ 求A，B两点间的距离 $($ 结果精确到 $0.1 km)$ ．
$($ 参考数据： $sin 34^{\circ} = 0.56$ ， $cos 34^{\circ} = 0.83$ ， $tan 34^{\circ} = 0.67.)$

查看试题解析
19. 在求 $1 + 3 + 3^{2} + 3^{4} + 3^{5} + 3^{6} + 3^{7} + 3^{8}$ 的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设： $S = 1 + 3 + 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6} + 3^{7} + 3^{8} ①$ ，然后在 $①$ 式的两边都乘以3，得： $3 S = 3 + 3^{2} + 3^{3} + 3^{4} + 3^{5} + 3^{6} + 3^{7} + 3^{8} + 3^{9} ②$ ， $② - ①$ 得： $3 S - S = 3^{9} - 1$ ，即 $2 S = 3^{9} - 1$ ， $∴ S = \frac{3^{9} - 1}{2}$ ．
请阅读张红发现的规律，并帮张红解决下列问题：

(1)、爱动脑筋的张红想：如果把“3”换成字母 $m (m \neq 0$ 且 $m \neq 1)$ ，应该能用类比的方法求出 $1 + m + m^{2} + m^{3} + m^{4} + \dots + m^{2018}$ 的值，对该式的值，你的猜想是 $($ 用含m的代数式表示 $)$ ．

(2)、证明你的猜想是正确的．

查看试题解析
20. 如图，在平面直角坐标系中，将坐标原点O沿x轴向左平移2个单位长度得到点A，过点A作y轴的平行线交反比例函数 $y = \frac{k}{x}$ 的图象于点B， $AB = \frac{3}{2}$ ．

(1)、求反比例函数的解析式；

(2)、若 $P (x_{1} ， y_{1})$ 、 $Q (x_{2} ， y_{2})$ 是该反比例函数图象上的两点，且 $x_{1} < x_{2}$ 时， $y_{1} > y_{2}$ ，指出点P、Q各位于哪个象限？并简要说明理由．

查看试题解析
21. 如图所示，在 $△ ABC$ 中， $∠ ACB = 90^{\circ}$ ，O是边AC上一点，以O为圆心，OA为半径的圆分别交AB，AC于点E，D，在BC的延长线上取点F，连接EF交AC于点G．

(1)、若 $BF = EF$ ，试判断直线EF与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $OA = 2$ ， $∠ A = 30^{\circ}$ ，求弧DE的长．

查看试题解析
22. 青岛市某大酒店豪华间实行淡季、旺季两种价格标准，旺季每间比淡季上涨 $\frac{1}{3}$ ，下表是去年该酒店豪华间某两天的相关记录：

旺季

淡季

未入住房间数

10

0

日总收入（元）

24 000

40 000

(1)、该酒店豪华间有多少间？旺季每间价格为多少元

(2)、今年旺季来临，豪华间的间数不变。经市场调查发现，如果豪华间仍旧实行去年旺季价格，那么每天都客满；如果价格继续上涨，那么每增加25元，每天未入住房间数增加1间。不考虑其他因素，该酒店将豪华间的价格上涨多少元时，豪华间的日总收入最高？最高日总收入是多少元？

查看试题解析
23. 平面直角坐标系xOy中，点A、B的横坐标分别为a、 $a + 2$ ，二次函数 $y = - x^{2} + (m - 2) x + 2 m$ 的图象经过点A、B，且a、m满足 $2 a - m = d (d$ 为常数 $)$ ．

(1)、若一次函数 $y_{1} = kx + b$ 的图象经过A、B两点．
$①$ 当 $a = 1$ 、 $d = - 1$ 时，求k的值；

$②$ 若y随x的增大而减小，求d的取值范围；

(2)、当 $d = - 4$ 且 $a \neq - 2$ 、 $a \neq - 4$ 时，判断直线AB与x轴的位置关系，并说明理由；

(3)、点A、B的位置随着a的变化而变化，设点A、B运动的路线与y轴分别相交于点C、D，线段CD的长度会发生变化吗？如果不变，求出CD的长；如果变化，请说明理由．

查看试题解析

	旺季	淡季
未入住房间数	10	0
日总收入（元）	24 000	40 000