广西北部湾经济区2018届数学中考模拟试卷

试卷更新日期：2018-12-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 若a+b＜0，a＜0，b＞0，则a，﹣a，b，﹣b的大小关系是（）

A、a＜﹣b＜b＜﹣a B、﹣b＜a＜﹣a＜b C、a＜﹣b＜﹣a＜b D、﹣b＜a＜b＜﹣a

查看试题解析
2. 如图放置的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 某种病毒近似于球体，它的半径约为0.000000005米，用科学记数法表示为（）

A、5×10⁸ B、5×10⁹ C、5×10^﹣8 D、5×10^﹣9

查看试题解析
4. 有以下图形：平行四边形、矩形、等腰三角形、线段、菱形，其中既是轴对称图形又是中心对称图形的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
5. 下列计算正确的是（）

A、a⁴+a²=a⁶ B、2a•4a=8a C、（a²）³=a⁵ D、a⁵÷a²=a³

查看试题解析
6. 如图，△ABC内接于⊙O，若∠A=α，则∠OBC等于（）

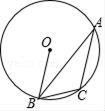A、90°﹣2α B、90°﹣α C、2α D、45°+α

查看试题解析
7. 不等式-2x+6>0的正整数解有（）

A、无数个 B、0个 C、1个 D、2个

查看试题解析
8. 如图，已知△ABC的面积为12，点D在线段AC上，点F在线段BC的延长线上，且BC=4CF，四边形DCFE是平行四边形，则图中阴影部分的面积为（）

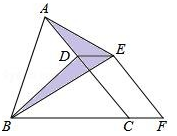A、2 B、3 C、4 D、6

查看试题解析
9. 已知一组数据：6，2，8， $x$ ，7，它们的平均数是6．则这组数据的中位数是（）

A、7 B、6 C、5 D、4

查看试题解析
10. 飞机着陆后滑行的距离s（米）关于滑行的时间t（米）的函数解析式是s=60t﹣1.5t² ，则飞机着陆后滑行到停止下列，滑行的距离为（）

A、500米 B、600米 C、700米 D、800米

查看试题解析
11. 如图，在平面直角坐标系中，点A在第二象限，⊙A分别与x轴、y轴相切．若将⊙A向右平移5个单位，圆心A恰好落在直线y=2x﹣4上，则⊙A的半径为（）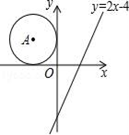

A、 B、2 C、4 D、6

查看试题解析
12. 如图，将直线y=x向下平移b个单位长度后得到直线l，l与反比例函数y= $\frac{k}{x}$ （k＞0，x＞0）的图象相交于点A，与x轴相交于点B，则OA²﹣OB²=10，则k的值是（）

A、5 B、10 C、15 D、20

查看试题解析

二、填空题

13. 一名学生军训时连续射靶10次，命中的环数分别为4，7，8，6，8，5，9，10，7，8．则这名学生射击环数的众数是．

查看试题解析
14. 如图， $a$ ∥ $b$ ，AB⊥ $a$ ，BC与 $b$ 相交，若∠ABC＝130°，则∠1＝°.

查看试题解析
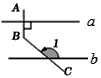15. 分解因式：3x²﹣6x²y+3xy²= ．

查看试题解析
16. 如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是线段BO上的一个动点，点F为射线DC上一点，若∠ABC=60°，∠AEF=120°，AB=4，则EF可能的整数值是．

查看试题解析
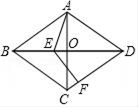17. 观察下列图形的排列规律（其中☆、□、●分别表示五角星、正方形、圆）●□☆●●□☆●□☆●●□☆●…若第一个图形是圆，则第2009个图形是（填名称）．

查看试题解析
18. 在正方形ABCD中，点E是AD的中点，连接BE，BF平分∠EBC交CD于点F，交AC于点G，将△CGF沿直线GF折叠至△C′GF，BD与△C′GF相交于点M、N，连接CN，若AB=6，则四边形CNC′G的面积是．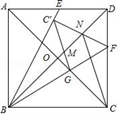

查看试题解析

三、解答题

19. 计算：（﹣1）²﹣2sin45°+（π﹣2018）⁰+|﹣ $\sqrt{2}$ |

查看试题解析
20. 如图，在10×10正方形网格中，每个小正方形的边长均为1个单位．将△ABC向下平移4个单位，得到△A′B′C′，再把△A′B′C′绕点C'顺时针旋转90°，得到△A″B″C′，

(1)、请你画出△A′B′C′和△A″B″C′（不要求写画法）．

(2)、求出线段A′C′在旋转过程中所扫过的面积．（结果保留）

查看试题解析
21. 如图是某校甲班学生外出去基地参观，乘车、行步、骑车的人数分布直方图和扇形统计图．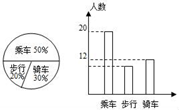

(1)、根据统计图求甲班步行的人数；

(2)、甲班步行的对象根据步行人数通过全班随机抽号来确定；乙班学生去基地分两段路走，即学校﹣﹣A地﹣﹣基地，每段路走法有乘车或步行或骑车，你认为哪个班的学生有步行的可能性少？（利用列表法或树状图求概率说明）．

查看试题解析
22. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC，AC交于点D，E．过点D作DF⊥AC交AC于点F．

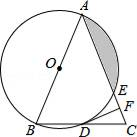(1)、求证：DF是⊙O的切线；

(2)、若⊙O的半径为8，∠CDF=22.5°，求阴影部分的面积．

查看试题解析
23. A、B两辆汽车同时从相距330千米的甲、乙两地相向而行，s（千米）表示汽车与甲地的距离，t（分）表示汽车行驶的时间，如图，L₁ ， L₂分别表示两辆汽车的s与t的关系．

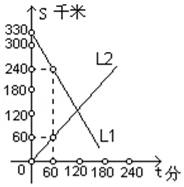(1)、L₁表示哪辆汽车到甲地的距离与行驶时间的关系？

(2)、汽车B的速度是多少？

(3)、求L₁ ， L₂分别表示的两辆汽车的s与t的关系式．

(4)、2小时后，两车相距多少千米？

(5)、行驶多长时间后，A、B两车相遇？

查看试题解析
24. 如图，在△ABC中，∠ACB=90°，∠ABC=30°，△CDE是等边三角形，点D在边AB上．

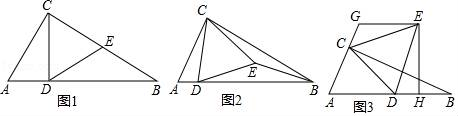(1)、如图1，当点E在边BC上时，求证DE=EB；

(2)、如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

(3)、如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG=5CG，BH=3．求CG的长．

查看试题解析
25. 如图1，在平面直角坐标系xOy中，直线l： $y = \frac{3}{4} x + π$ 与x轴、y轴分别交于点A和点B（0，﹣1），抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点B，且与直线l的另一个交点为C（4，n）．

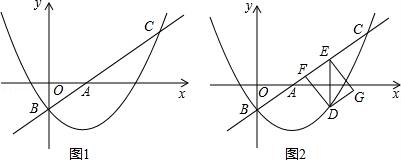(1)、求n的值和抛物线的解析式；

(2)、点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；

(3)、M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A₁O₁B₁ ，点A、O、B的对应点分别是点A₁、O₁、B₁ ．若△A₁O₁B₁的两个顶点恰好落在抛物线上，请直接写出点A₁的横坐标．

查看试题解析