江苏省扬州市江都区2018-2019学年七年级上学期数学期中考试试卷
试卷更新日期:2018-12-28 类型:期中考试
一、单选题
-
1. 的绝对值是( )A、 B、
 C、2
D、﹣2
2. 代数式 , , , 中,是整式的有( )A、1个 B、2个 C、3个 D、4个3. 下列说法中,正确的是( )A、两个有理数的和一定大于每个加数 B、3与- 互为倒数 C、0没有倒数也没有相反数 D、绝对值最小的数是04. 一名粗心的同学在进行加法运算时,将“-5”错写成“+5”进行运算,这样他得到的结果比正确答案( )A、少5 B、少10 C、多5 D、多105. 多项式 x|m|−(m−4)x+7是关于x的四次三项式,则m的值是( )
C、2
D、﹣2
2. 代数式 , , , 中,是整式的有( )A、1个 B、2个 C、3个 D、4个3. 下列说法中,正确的是( )A、两个有理数的和一定大于每个加数 B、3与- 互为倒数 C、0没有倒数也没有相反数 D、绝对值最小的数是04. 一名粗心的同学在进行加法运算时,将“-5”错写成“+5”进行运算,这样他得到的结果比正确答案( )A、少5 B、少10 C、多5 D、多105. 多项式 x|m|−(m−4)x+7是关于x的四次三项式,则m的值是( )
A、4 B、-2 C、-4 D、4或-46. 已知 ,且 ,则x等于( )A、-1 B、-2 C、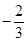 D、
D、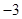 7. 已知 有最大值,则方程 的解是
7. 已知 有最大值,则方程 的解是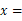 ( ) A、
( ) A、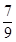 B、
B、 C、-
C、- 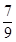 D、-
D、-  8. 用火柴棒按如图所示方式搭图形,按照这种方式搭下去,搭第9个图形需火柴棒的根数是( )
8. 用火柴棒按如图所示方式搭图形,按照这种方式搭下去,搭第9个图形需火柴棒的根数是( ) A、48 B、54 C、60 D、以上都不对
A、48 B、54 C、60 D、以上都不对二、填空题
-
9. 若将顺时针旋转60°记为-60°,则逆时针旋转45°可记为 .10. 已知2,-3,-4,6四个数,取其中的任意三个数求和,和最小是 .11. 已知 ,则 .12. 定义新运算: ? ,例如3?2=32+2=11,已知4? ,则 .13. 若 和 是同类项,则 .14. a、b两数的平方差除以a与b的差的平方,用代数式表示是.15. 已知 是方程 的解,则 的值为.16. 已知代数式x+2y的值是3,则代数式3-2x-4y的值是 .17. 在数轴上表示a、b两数的点如图所示,则 .
 18. 一列数,按如下规律排列:
18. 一列数,按如下规律排列:, , , , ,
则第 个数为 .
三、解答题
-
19. 计算:(1)、(2)、20. 先化简,再求值: ,其中 .21. 已知 , .(1)、求3A+6B;(2)、若3A+6B的值与 无关,求 的值.22. 解方程:(1)、(2)、23. 一个三角形的一边长为 ,另一边长比这条边长b,第三边长比这条边短 .(1)、求这个三角形的周长;(2)、若 , ,求三角形的周长.24. 某位同学做一道题:已知两个多项式A,B,求 的值.他误将 看成 ,求得结果为 ,已知 .(1)、求多项式A;(2)、求A-B的正确答案.25. 已知关于 的方程 和 有相同的解,那么这个解是什么?26. 已知 ,求:(1)、a+b+c+d+e+f 的值;(2)、 的值.27. 观察下列等式:
第1个等式: = = ×(1- );
第2个等 式: = = ×( - );
第3个等式: = = ×( - );第4个等式: = = ×( - ); …
请回答下列问题:
(1)、按以上规律列出第5个等式: ==;(2)、用含n的代数式表示第n个等式: ==(n为正整数);(3)、求 的值.28. 在一次数学社团活动中,指导老师给同学们提出了以下问题:问题:有67张卡片叠在一起,按从上而下的顺序先把第一张拿走,把第二张放到底层,然后把第三张拿走,再把第四张放到底层,如此进行下去,直至只剩最后一张卡片.问仅剩的这张卡片是原来的第几张卡片?
由于卡片数量较多,指导老师建议同学们先对较少的张数进行尝试,以便熟悉游戏规则并发现一些规律!请你也试着在草稿纸上进行试验,填写相应结果:
(1)、起初有2张卡片,按游戏规则最后剩下的卡片是原来的第张;(2)、起初有4张卡片,按游戏规则最后剩下的卡片是原来的第张;(3)、起初有8张卡片,按游戏规则最后剩下的卡片是原来的第张.(4)、根据试验结果进行规律总结,直接判断若起初有64张卡片,最后剩下的卡片是原来的第张.回到最初的67张卡片情形,请你给出答案并简要说明理由.