陕西省宝鸡市岐山县2019届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-28 类型:期中考试
一、单选题
-
1. 方程x2﹣2x﹣4=0的根的情况( )A、只有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根2. 袋中有8个红球和若干个黑球,小强从袋中任意摸出一球,记下颜色后又放回袋中,摇匀后又摸出一球,再记下颜色,做了50次,共有16次摸出红球,据此估计袋中有黑球( )个.A、15 B、17 C、16 D、183. 用配方法解方程3x2﹣6x+1=0,则方程可变形为( )A、(x﹣3)2= B、3(x﹣1)2= C、(3x﹣1)2=1 D、(x﹣1)2=4. 岐山县各学校开展了第二课堂的活动,在某校国学诗词组、篮球足球组、陶艺茶艺组三个活动组织中,若小斌和小宇两名同学每人随机选择其中一个活动参加,则小斌和小宇选到同一活动的概率是( )A、 B、 C、 D、
 5. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为( )
5. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为( )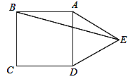 A、10° B、15° C、20° D、125°6. 顺次连接对角线相等的四边形各边中点所得四边形是( )A、矩形 B、平行四边形 C、菱形 D、任意四边形7. 一个不透明的口袋里装有分别标有汉字“陕”、“西”、“美”、“丽”的4个小球,除汉字不同之外,小球没有任何区别,小航从中任取两球,则取出的两个球上的汉字恰能组成“陕西”或“美丽”的概率是( )A、 B、 C、 D、8. 某市体育局要组织一次篮球邀请赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,设应邀请x个球队参加比赛,则可列方程为( )A、(x−1)x=28 B、(x+1)x=28 C、 (x−1)x=28 D、
A、10° B、15° C、20° D、125°6. 顺次连接对角线相等的四边形各边中点所得四边形是( )A、矩形 B、平行四边形 C、菱形 D、任意四边形7. 一个不透明的口袋里装有分别标有汉字“陕”、“西”、“美”、“丽”的4个小球,除汉字不同之外,小球没有任何区别,小航从中任取两球,则取出的两个球上的汉字恰能组成“陕西”或“美丽”的概率是( )A、 B、 C、 D、8. 某市体育局要组织一次篮球邀请赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,设应邀请x个球队参加比赛,则可列方程为( )A、(x−1)x=28 B、(x+1)x=28 C、 (x−1)x=28 D、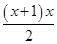 =28
9. 正方形具有而菱形不一定具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角10. 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
=28
9. 正方形具有而菱形不一定具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角10. 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )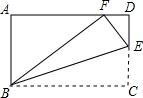 A、2 B、 C、1 D、
A、2 B、 C、1 D、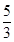
二、填空题
-
11. 若m、n是一元二次方程x2﹣5x﹣2=0的两个实数根,则m+n﹣mn= .12. 如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的 ,则路宽x应满足的方程是 .
 13. 如图, 为正方形 的对角线,延长 到 ,使 ,以 为一边作菱形 ,若菱形的面积为 ,则正方形边长 .
13. 如图, 为正方形 的对角线,延长 到 ,使 ,以 为一边作菱形 ,若菱形的面积为 ,则正方形边长 .
三、解答题
-
14. 如图:电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光。
 (1)、任意闭合其中一个开关,则小灯泡发光的概率等于__;(2)、任意闭合其中两个开关,请用画树状图或列表的方法求出小
(1)、任意闭合其中一个开关,则小灯泡发光的概率等于__;(2)、任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
15. 用适当的方法解下列方程:(1)、x2+x−2=0;(2)、x−3=x(x−3)16. 如图,已知△ABC中,∠ABC=90°. (1)、尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
(1)、尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)、判断四边形ABCD的形状,并说明理由.17. 为了巩固全国文明城市建设成果,突出城市品质的提升,近年来,我市积极落实节能减排政策,推行绿色建筑,据统计,我市2016年的绿色建筑面积约为950万平方米,2018年达到了1862万平方米.若2017年、2018年的绿色建筑面积按相同的增长率逐年递增,请解答下列问题:(1)、求这两年我市推行绿色建筑面积的年平均增长率;(2)、2019年我市计划推行绿色建筑面积达到2400万平方米.如果2019年仍保持相同的年平均增长率,请你预测2019年我市能否完成计划目标?18. 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.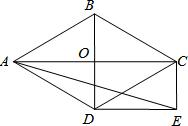 (1)、求证:四边形ODEC是矩形;(2)、当∠ADB=60°,AD=2 时,求EA的长。19. 如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)、求证:四边形ODEC是矩形;(2)、当∠ADB=60°,AD=2 时,求EA的长。19. 如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.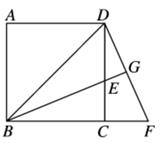 (1)、求证:△BCE≌△DCF;(2)、求CF的长。20. 在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.(1)、从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;(2)、分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.21. 已知:平行四边形ABCD的两边AB、AD的长是关于x的方程x2﹣mx+ - =0的两个实数根.(1)、m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)、若AB的长为2,那么平行四边形ABCD的周长是多少?22. 商场某种商品平均每天可销售
(1)、求证:△BCE≌△DCF;(2)、求CF的长。20. 在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.(1)、从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;(2)、分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.21. 已知:平行四边形ABCD的两边AB、AD的长是关于x的方程x2﹣mx+ - =0的两个实数根.(1)、m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)、若AB的长为2,那么平行四边形ABCD的周长是多少?22. 商场某种商品平均每天可销售 件,每件盈利
件,每件盈利  元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价
元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价  元,商场平均每天可多售出
元,商场平均每天可多售出  件.
件.  若某天该商品每件降价
若某天该商品每件降价  元,当天可获利多少元?(1)、 若某天该商品每件降价
元,当天可获利多少元?(1)、 若某天该商品每件降价 元,当天可获利多少元? (2)、
元,当天可获利多少元? (2)、设每件商品降价
 元,则商场日销售量增加件,每件商品,盈利元(用含
元,则商场日销售量增加件,每件商品,盈利元(用含  的代数式表示);(3)、
的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到
 元?23. 如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
元?23. 如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF. (1)、求证:△AED≌△CFD;(2)、求证:四边形AECF是菱形.(3)、若AD=3,AE=5,则菱形AECF的面积是多少?
(1)、求证:△AED≌△CFD;(2)、求证:四边形AECF是菱形.(3)、若AD=3,AE=5,则菱形AECF的面积是多少?