湖北省宜城市2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-28 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} + 2 x - \frac{5}{4} = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
2. 若一元二次方程 $x^{2} + b x + 5 = 0$ 配方后为 ${(x - 3)}^{2} = k$ ，则b，k的值分别为（）

A、-6，4 B、6，4 C、6，13 D、-6，13

查看试题解析
3. 已知一元二次方程 $x^{2} + k x - 3 = 0$ 有一个根为-1，则k的值为（）

A、2 B、-2 C、4 D、-4

查看试题解析
4. 与抛物线 $y = - \frac{1}{3} x^{2} + 2 x - 7$ 的形状、开口方向都相同，只有位置不同的抛物线是（）

A、 B、 C、 D、

查看试题解析
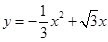5. 下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转90°后，能与原图形完全重合的是（）

A、 B、 C、 D、

查看试题解析
6. 若直线 $y = m x + n$ 经过第一、二、四象限，则抛物线 $y = {(x - m)}^{2} + n$ 的顶点必在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，在Rt△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B'，点C的对应点是点C')，连接CC'，若∠B =78°，则∠CC'B'的大小是（）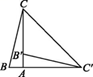

A、23° B、30° C、33° D、39°

查看试题解析
8. 如图，AB是⊙O的直径，弦CD⊥AB于点E，AB=20cm，CD=12cm，则BE=（）

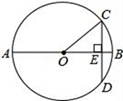A、6cm B、5cm C、3cm D、2cm

查看试题解析
9. 如图，⊙O中，弦BC与半径OA相交于点D，连接AB，OC．若∠C=35°，∠ADC=85°，则∠A的度数是（）

A、50° B、55° C、60° D、70°

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，若M= $4 a - 2 b + c$ ，N= $a + b + c$ ，则（）

A、M>0，N>0 B、M>0，N<0 C、M<0，N>0 D、M<0，N<0

查看试题解析

二、填空题

11. 关于x的一元二次方程x²﹣4x+3=0的解为.

查看试题解析
12. 为提高学生足球水平，某市将开展足球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排28场比赛，应邀请多少个球队参赛？

查看试题解析
13. 二次函数 $y = x^{2} + 4 x + 3$ 的图象是由 $y = a x^{2} + b x + c$ 的图象向右平移1个单位，再向下平移2个单位得到的，则a= ， b= ， c= ．

查看试题解析
14. 如图，已知正方形ABCD的边长为 $2 \sqrt{2}$ ，E为CD边上一点，DE＝1，以点A为中心，把△ADE顺时针旋转90°，得△ABE′，连接EE′，则EE′的长等于．

查看试题解析
15. 如图所示，某公园的一座石拱桥是圆弧形(劣弧)，其跨度为12m，拱的半径为10m，则拱高为m.

查看试题解析
16. 如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作 $⊙ P .$ 当 $⊙ P$ 与正方形ABCD的边相切时，BP的长为．

查看试题解析
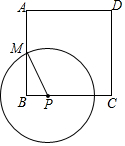17. 如图，某市近郊有一块长为60米，宽为50米的矩形荒地，地方政府准备在此建一个综合性休闲广场，其中阴影部分为通道，通道的宽度均相等，中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地．

(1)、设通道的宽度为x米，则a＝(用含x的代数式表示)；

(2)、若塑胶运动场地总占地面积为2430米² ，则通道的宽度为多少米？

查看试题解析

三、解答题

18. 解方程：x²+2x﹣1=0．

查看试题解析
19. 如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．

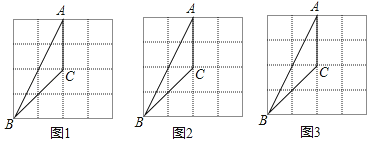(1)、在图1中，画出一个与△ABC成中心对称的格点三角形；

(2)、在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；

(3)、在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形．

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ 是 $\overset{⌢}{B D}$ 的中点， $C E ⊥ A B$ 于点 $E$ ， $B D$ 交 $C E$ 于点 $F$ ．

(1)、求证： $C F = B F$ ；

(2)、若 $C D ﹦ 5$ ， $A C ﹦ 12$ ，求 $⊙ O$ 的半径和 $C E$ 的长．

查看试题解析
21. 如图，二次函数的图象与 $x$ 轴交于点 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ，交 $y$ 轴于点 $C (0 ， 3)$ ，点 $C$ ， $D$ 是二次函数图象上关于抛物线对称轴的一对对称点，一次函数的图象过点 $B$ ， $D$ ．

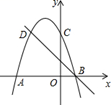(1)、请直接写出点 $D$ 的坐标；

(2)、求二次函数的解析式；

(3)、根据图象直接写出一次函数值大于二次函数值的 $x$ 的取值范围．

查看试题解析
22. 如图，已知⊙O的半径为1，AC是⊙O的直径，过点C作⊙O的切线BC，E是BC的中点，AB交⊙O于D点．

(1)、直接写出ED和EC的数量关系：；

(2)、DE是⊙O的切线吗？若是，给出证明；若不是，说明理由；

(3)、填空：当BC=时，四边形AOED是平行四边形，同时以点O、D、E、C为顶点的四边形是．

查看试题解析
23. 某水晶厂生产的水晶工艺品非常畅销，某网店专门销售这种工艺品.成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，当x=40时，y=300；当x=55时，y=150．

(1)、求y与x之间的函数关系式；

(2)、如果规定每天工艺品的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该工艺品销售单价的范围．

查看试题解析
24. 如图，已知∠AOB=120°，在∠AOB的平分线OM上有一点C，将一个60°角的顶点与点C重合，它的两条边分别与直线OA、OB相交于点D、E．

(1)、当∠DCE绕点C旋转到CD与OA垂直时（如图1），请猜想OE+OD与OC的数量关系，并说明理由；

(2)、当∠DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；

(3)、当∠DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明．

查看试题解析
25. 如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x + c$ （a≠0）与x轴交于A（﹣1，0）、B（﹣3，0）两点，与y轴交于点C（0，﹣3），其顶点为点D，点E的坐标为（0，﹣ $\frac{3}{2}$ ），该抛物线与BE交于另一点F，连接BC．

(1)、求该抛物线的解析式，并用配方法把解析式化为 $y = a {(x - h)}^{2} + k$ 的形式；

(2)、动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM，BM，当t为何值时，△OMB为等腰三角形？

(3)、在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析