广西桂林市灌阳县2019届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-28 类型：期中考试

进入出卷网下载

一、单选题

1. 若反比例函数 $y = \frac{k}{x}$ （k≠0）的图象经过点（-1，3），则此函数图象一定经过点（）

A、（ $\fr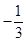ac{1}{3}$ ，3） B、（，3） C、（-3，-1） D、（3，-1）

查看试题解析
2. 下列方程中，是关于 $x$ 的一元二次方程的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在△ABC中，若DE∥BC， $\frac{A D}{A B} = \frac{1}{3}$ ，BC = 12 cm，则DE的长为（）

A、12cm B、6 cm C、4cm D、3 cm

查看试题解析
4. 如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D，E，F分别是OA， OB， OC的中点，则△DEF与△ABC的面积比是（）

A、1：6 B、1：5 C、1：4 D、1：2

查看试题解析
5. 若关于 $x$ 的一元二次方程 $a x^{2} + b x + 5 = 0$ （ $a$ ≠0）的解是 $x$ = 1，则 $a$ + $b$ 的值是（）

A、5 B、-5 C、6 D、-6

查看试题解析
6. 把方程 $x^{2} + 3 x - 1 = 0$ 的左边配方后可得方程（）

A、 B、 C、 D、

查看试题解析
7. 一元二次方程 $x^{2} - 4 x + 5 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8. 若关于 $x$ 的一元二次方程 ${kx}^{2} - 4 x + 3 = 0$ 有实数根，则 $k$ 的非负整数值是（）

A、1 B、0,1 C、1,2 D、1,2,3

查看试题解析
9. 九年级（1）班有若干人，新年互送贺年卡一张，已知全班共送贺年卡2970张，则这个班共有（）

A、54人 B、55人 C、56人 D、57人

查看试题解析
10. 如图，路灯距地面8米，身高1.6米的小李从点A处沿AO所在的直线行走14米到点B时，人影长度（）

A、变长3.5米 B、变长2.5米 C、变短3.5米 D、变短2.5米

查看试题解析
11. 如图，函数 $y_{1} = x - 1$ 和函数 $y_{2} = \frac{2}{x}$ 的图象相交于点M(2，m)，N(-1，n)，若 $y_{1} > y_{2}$ ，则x的取值范围是（）

A、或； B、或； C、 $- 1 < x < 0$ 或； D、 $- 1 < x < 0$ 或；

查看试题解析
12. 如图，梯形AOBC中，对角线交于点E，双曲线y= $\frac{k}{x}$ （k＞0）经过A，E两点，若AC ： OB = 1：3，梯形AOBC面积为24，则k =（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 方程 $x^{2} - 4 x = 0$ 的解为.

查看试题解析
14. 已知 $a$ ， $b$ ， $c$ ， $d$ 是成比例线段，其中 $a$ =5， $b$ =4， $c$ =10，线段 $d$ =.

查看试题解析
15. 已知△ABC∽△DEF，且相似比为3：4，S_△ABC=2cm² ，则S_△DEF=

查看试题解析
16. 如图，l₁∥l₂∥l₃ ，两条直线与这三条平行线分别交于点A、B、C和D、E、F，已知 $\frac{A B}{B C}$ ＝ $\frac{4}{3}$ ，若DF＝10，则DE＝．

查看试题解析
17. 点C把线段AB分成两条线段AC和BC（AC＞BC），如果 $\frac{A C}{A B} = \frac{B C}{A C}$ ，那么称线段AB被点C黄金分割，AC与AB的比叫作黄金比，其比值为.

查看试题解析
18. 已知 $α$ 、 $β$ 是关于 $x$ 的一元二次方程 $x^{2} + (2 m + 3) x + m^{2} = 0$ 的两个不相等的实数根，且满足 $\frac{1}{α} + \frac{1}{β} = - 1$ ，则 $m$ 的值是．

查看试题解析

三、解答题

19. 解方程:

(1)、 ${(x + 1)}^{2} - 9 = 0$

(2)、 $2 x^{2} - 4 x - 1 = 0$

查看试题解析
20. 先化简再求值： $\frac{x - 3}{3 x^{2} - 6 x} \div (x + 2 - \frac{5}{x - 2})$ ，其中 $x$ 满足 $x^{2} - 3 x + 2 = 0$ .

查看试题解析
21. 如图，已知△ABC的三个顶点坐标如下表：

(1)、将下表补充完整，并在直角坐标系中，画出△A′B′C′；

（x，y）

（2x，2y）

A（2，1）

A′（4，2）

B（4，3）

B′

C（5，1）

C′

(2)、观察两个三角形，可知△ABC∽△A′B′C′两个三角形的是以原点为位似中心的位似三角形，△ABC与△A′B′C′的位似比为.

查看试题解析
22. $m$ 为任意实数，请证明关于 $x$ 的方程 $x^{2} - (m - 1) x - 3 (m + 3) = 0$ 恒有两个不相等的实数根，并任意给出 $m$ 的一个值，求出方程的根。

查看试题解析
23. 某品牌计算机春节期间搞活动，规定每台计算机售价 0.7 万元，首次付款后每个月应还的钱数 y （元）与还钱月数 t 的关系如图所示．

(1)、根据图像写出 y 与 t 的函数关系式；

(2)、求出首次付款的钱数；

(3)、如果要求每月支付的钱数不多于 400 元，那么首付后还至少需几个月才能将所有的钱全部还清？

查看试题解析
24. 如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F.求证： $A B \cdot A D = E A \cdot B F$

查看试题解析
25. 桂林市新建的汽车南站站前广场需要绿化。该项绿化工程中有一块长为20 m，宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56m² ，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？

查看试题解析
26. 如图所示，在平面直角坐标中，四边形OABC是梯形，且AB = OC = 4，CB∥OA，OA = 7，∠COA = 60°，点P为x轴上的—个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于点D，

(1)、求点B的坐标；

(2)、当点P运动什么位置时，使得∠CPD =∠OAB，且 $\frac{B D}{B A} = \frac{5}{8}$ ，求这时点P的坐标；

(3)、当点P运动什么位置时，△OCP为等腰三角形，直接写出这时点P的坐标。

查看试题解析

（x，y）	（2x，2y）
A（2，1）	A′（4，2）
B（4，3）	B′
C（5，1）	C′