2017年浙江省数学中考模拟卷(三)
试卷更新日期:2017-04-06 类型:中考模拟
一、选择题:
-
1. 下列各选项中,既不是正数也不是负数的是( )A、-1 B、0 C、1 D、2. 用代数式表示“2m与5的差”为( )A、 2m-5 B、 5-2m C、 2(m-5) D、 2(5-m)3. 已知 , 则代数式的值为( )A、 B、 C、 D、4.
等于( ).
A、 B、 C、 D、5. 二元一次方程组 的解为( )
的解为( )
A、 B、
B、 C、
C、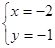 D、
D、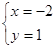 6.
6.将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )
 A、考 B、试 C、成 D、功7. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )A、当AB=BC时,它是菱形 B、当AC=BD时,它是正方形 C、当AC⊥BD时,它是菱形 D、当∠ABC=90°时,它是矩形8. 在Rt 中,∠C= 90°,若 则 的值是 ( )A、 B、 C、 D、9. 在平面直角坐标系中,已知直线y=- x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A、(0, ) B、(0, ) C、(0,3) D、(0,4)10. 如图所示,一般书本的纸张是在原纸张多次对开得到.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推.若各种开本的矩形都相似,那么 等于( ).
A、考 B、试 C、成 D、功7. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )A、当AB=BC时,它是菱形 B、当AC=BD时,它是正方形 C、当AC⊥BD时,它是菱形 D、当∠ABC=90°时,它是矩形8. 在Rt 中,∠C= 90°,若 则 的值是 ( )A、 B、 C、 D、9. 在平面直角坐标系中,已知直线y=- x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )A、(0, ) B、(0, ) C、(0,3) D、(0,4)10. 如图所示,一般书本的纸张是在原纸张多次对开得到.矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依此类推.若各种开本的矩形都相似,那么 等于( ).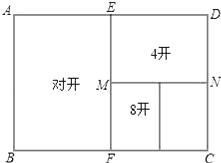 A、0.618 B、 C、 D、211. 若关于x的分式方程 无解,则m的值为( )A、-1.5 B、1 C、-1.5或2 D、-0.5或-1.512. 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A、0.618 B、 C、 D、211. 若关于x的分式方程 无解,则m的值为( )A、-1.5 B、1 C、-1.5或2 D、-0.5或-1.512. 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )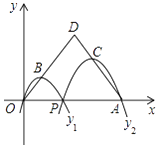 A、 B、 C、3 D、4
A、 B、 C、3 D、4二、填空题:
-
13. 若 ,则代数式 的值为 .
14. 已知 ,则 = .15. 如图,点A在双曲线y= 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为 ,则k的值为 .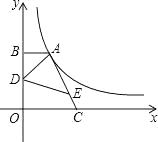 16. 如图,在平面直角坐标系中,点A(8,0),点P(0,m),将线段PA绕着点P逆时针旋转90°,得到线段PB,连接AB,OB,则BO+BA的最小值为 .
16. 如图,在平面直角坐标系中,点A(8,0),点P(0,m),将线段PA绕着点P逆时针旋转90°,得到线段PB,连接AB,OB,则BO+BA的最小值为 .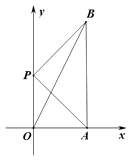
三、解答题:
-
17. 计算:18. 先化简,再求值: ,其中 是不等式组 的整数解19.
某学校为了解该校七年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):
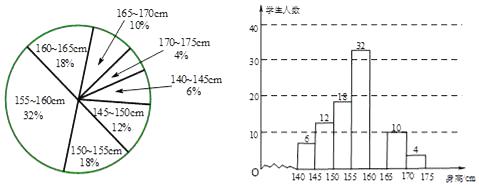 (1)、请根据所提供的信息计算身高在160~165cm范围内的学生人数,并补全频数分布直方图;
(1)、请根据所提供的信息计算身高在160~165cm范围内的学生人数,并补全频数分布直方图;
(2)、样本的中位数在统计图的哪个范围内?(3)、如果上述样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么(填“七年级”或“八年级”)学生的身高比较整齐.
20. 某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:x(单位:台)
10
20
30
y(单位:万元∕台)
60
55
50
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求该机器的生产数量;
(3)、市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)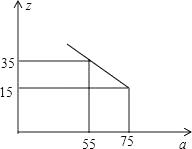 21. 如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.
21. 如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.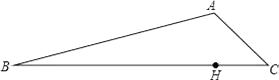
(1)、求BC的长度;(2)、如果两个分队在前往A地时匀速前行,且甲的速度是乙的速度的三倍.试判断哪个分队先到达A地.(tan55°≈1.4,sin55°≈0.84,cos55°≈0.6, ≈5.01,结果保留整数)
22. 如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.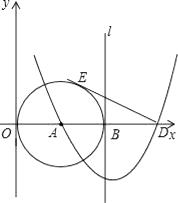
(1)、以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;(2)、在(1)的条件下,抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)、点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
23. 如图,在平面直角坐标系xOy中,二次函数y=﹣ +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣ +bx+c的图象分别交于B,C两点,点B在第一象限.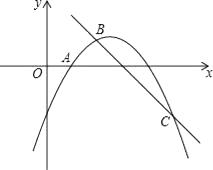
(1)、求二次函数y=﹣ +bx+c的表达式;(2)、连接AB,求AB的长;(3)、连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.