2018-2019学年初中数学北师大版九年级下册1.1锐角三角函数同步练习

试卷更新日期：2018-12-27 类型：同步测试

进入出卷网下载

一、单选题

1. 在Rt△ABC中，∠C=90°，若斜边AB是直角边BC的3倍，则tanB的值是（）

A、2 $\sqrt{2}$ B、3 C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{1}{3}$

查看试题解析
2. 在△ABC中，∠A，∠B，∠C对边分别为a，b，c，a=5，b=12，c=13，下列结论成立的是（）

A、 $\sin A = \frac{12}{5}$ B、 $\cos A = \frac{5}{13}$ C、 $\tan A = \frac{5}{12}$ D、 $\cos B = \frac{12}{13}$

查看试题解析
3. 如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD=5，AC=6，则tan∠DCB的值是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
4. 如图，△ABC的顶点都在正方形网格的格点上，则cosC的值为（）

A、 $\frac{3 \sqrt{5}}{10}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{1}{2}$

查看试题解析
5. 在Rt△ABC中， $∠ C = 90 °$ ， $B C = a$ ， $A C = b$ ， $A B = c$ ，下列各式中正确的是（）

A、 $a = b \cdot cos A$ ； B、 $c = a \cdot sin A$ ； C、 $a \cdot cot A = b$ ； D、 $a \cdot tan A = b$ ．

查看试题解析
6. 在Rt $Δ$ ABC中，∠C=90°， $∠ A = α$ ，AC= $3$ ，则AB的长可以表示为（）

A、 $\frac{3}{cos α}$ B、 $\frac{3}{sin α}$ C、 $3 sin α$ D、 $3 cos α$

查看试题解析
7. 在△ABC中，∠C=90°，且两条直角边a，b满足a²﹣5ab+6b²=0，则tanA的值为（）

A、5或6 B、2 C、3 D、2或3

查看试题解析
8. Rt△ABC中，∠C=90°，已知cosA= $\frac{3}{5}$ ，那么tanA等于（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

查看试题解析
9. 如图，延长Rt△ABC斜边AB到D点，使BD=AB，连接CD，若cot∠BCD=3，则tanA=（）

A、 $\frac{3}{2}$ B、1 C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
10. 如图，在平面直角坐标系中，点A的坐标为(3，4)，那么sinα的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析

二、填空题

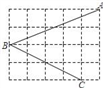
11. 在Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边，下列式子：①a=c•sinB，②a=c•cosB，③a=c•tanB，④a= $\frac{c}{tanB}$ ，必定成立的是．

查看试题解析
12. 用不等号“＞”或“＜”连接：sin50° cos50°．

查看试题解析
13. 如图所示方格纸中每个小正方形的边长为1，其中有三个格点A、B、C，则sin∠ABC= ．

查看试题解析
14. △ABC中，∠C=90°，tanA= $\frac{4}{3}$ ，则sinA+cosA= ．

查看试题解析
15. 阅读理解：已知∠A、∠B是Rt△ABC的两个锐角，锐角∠A的邻边与对边的比值叫做锐角∠A的余切，记作cotA，记cotA= $\frac{∠ A 的邻边}{∠ A 的邻边}$ ，已知tanB= $\frac{4}{3}$ ，则cotB的值等于．

查看试题解析
16. 如图，P是∠α的边OA上一点，且P点的坐标为（3，4），则sin（90°﹣α）= ．

查看试题解析

三、综合题

17. 已知，如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A、C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC= $\frac{3}{4}$ ．

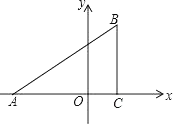(1)、求点B的坐标；

(2)、在x轴上找一点D，连接BD使得△ABD与△ABC相似（不包括全等），并求点D的坐标．

查看试题解析
18. 如图，E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE，点F落在AD上.

(1)、求证：△ABF∽△DFE；

(2)、若sin∠DFE= $\frac{1}{3}$ ，求tan∠EBC的值.

查看试题解析
19. 如图，已知∠ABC和射线BD上一点P（点P与点B不重合），且点P到BA、BC的距离为PE、PF．

(1)、若∠EBP=40°，∠FBP=20°，PB=m，试比较PE、PF的大小；

(2)、若∠EBP=α，∠FBP=β，α，β都是锐角，且α＞β．试判断PE、PF的大小，并给出证明．

查看试题解析
20. 如图，在等边△ABC 内有一点D，AD=5，BD=6，CD=4，将线段AD绕点A旋转到AE，使∠DAE=∠BAC，连接EC．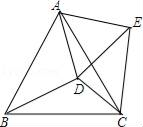

(1)、求CE的长；

(2)、求cos∠CDE的值．

查看试题解析
21. 在如图的直角三角形中，我们知道sinα= $\frac{a}{c}$ ，cosα= $\frac{b}{c}$ ，tanα= $\frac{a}{b}$ ，∴sin²α+cos²α= $\frac{a^{2}}{c^{2}}$ + $\frac{b^{2}}{c^{2}}$ = $\frac{a^{2} + b^{2}}{c^{2}}$ = $\frac{c^{2}}{c^{2}}$ =1．即一个角的正弦和余弦的平方和为1．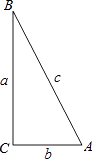

(1)、请你根据上面的探索过程，探究sinα，cosα与tanα之间的关系；

(2)、请你利用上面探究的结论解答下面问题：已知α为锐角，且tanα= $\frac{1}{2}$ ，求 $\frac{\sin α - 2 \cos α}{2 \sin α + \cos α}$ 的值．

查看试题解析
22. 如图

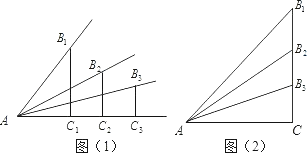(1)、如图，锐角的正弦和余弦都随着锐角的确定而确定，也随着其变化而变化，试探索随着锐角度数的增大，它的正弦值和余弦值的变化规律；

(2)、根据你探索到的规律，试比较18°，34°，52°，65°，88°，这些角的正弦值的大小和余弦值的大小；

(3)、比较大小：（在空格处填写“＜”或“＞”或“=”）
若∠α=45°，则sinαcosα；若∠α＜45°，则sinαcosα；若∠α＞45°，则sinαcosα；

(4)、利用互余的两个角的正弦和余弦的关系，比较下列正弦值和余弦值的大小：
sin10°，cos30°，sin50°，cos70°．

查看试题解析

2018-2019学年初中数学北师大版九年级下册1.1锐角三角函数 同步练习

一、单选题

二、填空题

三、综合题

2018-2019学年初中数学北师大版九年级下册1.1锐角三角函数同步练习