2018-2019学年初中数学浙教版九年级下册1.1锐角三角函数 同步练习
试卷更新日期:2018-12-27 类型:同步测试
一、单选题
-
1. 下列计算正确的是( )A、sin60°﹣sin30°=sin30° B、sin245°+cos245°=1 C、cos60 D、cos302. 在△ABC中,若tanA=1,sinB= ,你认为最确切的判断是( )
A、△ABC是等腰三角形 B、△ABC是等腰直角三角形 C、△ABC是直角三角形 D、△ABC是一般锐角三角形3. 在Rt△ABC中, , , , ,下列各式中正确的是( )A、 ; B、 ; C、 ; D、 .4. 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于 ( )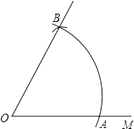 A、 B、 C、 D、5. 如图,正方形 中, 为 的中点, 为 上一点, ,设 ,则 的值等于( ).
A、 B、 C、 D、5. 如图,正方形 中, 为 的中点, 为 上一点, ,设 ,则 的值等于( ). A、 B、 C、 D、6. 点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )A、 B、 C、 D、7. 在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB的值等于( )A、 B、 C、 D、8. 如图,P是∠α的边OA上一点,点P的坐标为(12,5),则∠α的正弦值为( )
A、 B、 C、 D、6. 点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )A、 B、 C、 D、7. 在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB的值等于( )A、 B、 C、 D、8. 如图,P是∠α的边OA上一点,点P的坐标为(12,5),则∠α的正弦值为( ) A、 B、 C、 D、9. 因为cos60°= ,cos240°=﹣ ,所以cos240°=cos(180°+60°)=﹣cos60°;由此猜想、推理知:当α为锐角时有cos(180°+α)=﹣cosα,由此可知:cos210°=( )A、﹣ B、﹣ C、﹣ D、﹣10. 如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( )
A、 B、 C、 D、9. 因为cos60°= ,cos240°=﹣ ,所以cos240°=cos(180°+60°)=﹣cos60°;由此猜想、推理知:当α为锐角时有cos(180°+α)=﹣cosα,由此可知:cos210°=( )A、﹣ B、﹣ C、﹣ D、﹣10. 如图,在△ABC中,BC=10,∠B=60°,∠C=45°,则点A到BC的距离是( )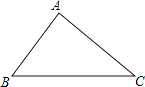 A、10﹣5 B、5+5 C、15﹣5 D、15﹣10
A、10﹣5 B、5+5 C、15﹣5 D、15﹣10二、填空题
-
11. 如图,在Rt△ABC中,∠ACB=90°,CD是高,如果∠A=α,AC=4,那么BD= . (用锐角α的三角比表示)
 12. 如图,∠A=120°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则sin(∠BPE+∠BCE)=
12. 如图,∠A=120°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则sin(∠BPE+∠BCE)= 13. 若α为锐角,且tan (90°-α)= ,则tan α=.14. 一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为 .15. 阅读理解:已知∠A、∠B是Rt△ABC的两个锐角,锐角∠A的邻边与对边的比值叫做锐角∠A的余切,记作cotA,记cotA= ,已知tanB= ,则cotB的值等于 .16. 已知α为锐角,当 无意义时,tan(α+15°)﹣tan(α﹣15°)的值是 .
13. 若α为锐角,且tan (90°-α)= ,则tan α=.14. 一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为 .15. 阅读理解:已知∠A、∠B是Rt△ABC的两个锐角,锐角∠A的邻边与对边的比值叫做锐角∠A的余切,记作cotA,记cotA= ,已知tanB= ,则cotB的值等于 .16. 已知α为锐角,当 无意义时,tan(α+15°)﹣tan(α﹣15°)的值是 .
三、解答题
-
17. 计算下面各题:
(1)、cos 60°-tan 45°+sin 30°;(2)、 -tan245°.18. 已知α为锐角,且 =2,求tan α的值.
19. 先化简,再求值:÷ ,其中x=2(tan45°-cos30°).
20. 计算:sin2 1°+sin2 2°+sin2 3°+…+sin2 87°+sin2 88°+sin2 89°
21. 下列关系式是否成立(0<α<90°),请说明理由.(1)、sinα+cosα≤1;(2)、sin2α=2sinα.22. 根据已知条件,判断△ABC的形状:
(1)、在△ABC中,若 + =0,判断△ABC的形状;(2)、已知a=3,且(4tan45°-b)2+ =0,判断以a,b,c为边组成的三角形的形状.
23. 如图: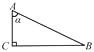 (1)、已知sinα+cosα= ,求sinαcosα.
(1)、已知sinα+cosα= ,求sinαcosα.
(2)、已知α为锐角,tanα=2,求 的值.
24. 【问题学习】小芸在小组学习时间小娟这样一个问题:已知α为锐角,且sinα= ,求sin2α的值.小娟是这样给小芸讲解的:构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ,可设BC=x,则AB=3x,….
 (1)、【问题解决】
(1)、【问题解决】请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)、如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ,求sin2β的值.