吉林省长春市2018年高考文数数学二模试卷
试卷更新日期:2018-12-27 类型:高考模拟
一、单选题
-
1. 已知 , ,则A、
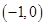 B、
B、 C、
C、 D、
D、 2. 已知复数 ,则A、
2. 已知复数 ,则A、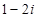 B、
B、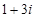 C、
C、 D、
D、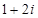 3. 命题“若 ,则 ”的逆否命题是A、若
3. 命题“若 ,则 ”的逆否命题是A、若 ,则
,则  且
且  B、若
B、若  ,则
,则  C、若
C、若  或
或  ,则
,则  D、若
D、若  或
或  ,则
,则  4. 已知椭圆 的左右焦点分别为 , ,过 且垂直于长轴的直线交椭圆于A,B两点,则 的周长为A、4 B、6 C、8 D、165. 已知平面向量 , ,则A、
4. 已知椭圆 的左右焦点分别为 , ,过 且垂直于长轴的直线交椭圆于A,B两点,则 的周长为A、4 B、6 C、8 D、165. 已知平面向量 , ,则A、 B、3
C、
B、3
C、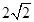 D、5
6. 已知等比数列 的各项均为正数,其前n项和为 ,若 , ,则A、4 B、10 C、16 D、327. 定义在R上的奇函数 ,满足在 上单调递增,且 ,则 的解集为A、
D、5
6. 已知等比数列 的各项均为正数,其前n项和为 ,若 , ,则A、4 B、10 C、16 D、327. 定义在R上的奇函数 ,满足在 上单调递增,且 ,则 的解集为A、 B、
B、 C、
C、 D、
D、 8. 如图,网格纸上小正方形的边长为1,粗线条画出的是一个三棱锥的三视图,则该三棱锥的体积为( )
8. 如图,网格纸上小正方形的边长为1,粗线条画出的是一个三棱锥的三视图,则该三棱锥的体积为( ) A、 B、 C、
A、 B、 C、 D、
9. 若点 满足线性条件 ,则 的最大值为( )A、
D、
9. 若点 满足线性条件 ,则 的最大值为( )A、 B、
B、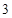 C、
C、 D、
D、 10. 已知函数 ,且 ,则下列结论中正确的是A、
10. 已知函数 ,且 ,则下列结论中正确的是A、 B、
B、 是
是  图象的一个对称中心
C、
图象的一个对称中心
C、 D、
D、 是
是  图象的一条对称轴
11. 已知双曲线 的左、右焦点分别为 , ,点P在双曲线的右支上,且 ,则双曲线离心率的取值范围是A、
图象的一条对称轴
11. 已知双曲线 的左、右焦点分别为 , ,点P在双曲线的右支上,且 ,则双曲线离心率的取值范围是A、 B、
B、 C、
C、 D、
D、 12. 若关于x的方程 存在三个不等实根,则实数a的取值范围是A、
12. 若关于x的方程 存在三个不等实根,则实数a的取值范围是A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 曲线 在点 处的切线方程为.14. 若向区域 内投点,则该点到原点的距离小于 的概率为.15. 更相减损术是出自 九章算术 的一种算法 如图所示的程序框图是根据更相减损术写出的,若输入 , ,则输出的值为 .
 16. 在△ 中,内角 的对边分别为 ,若其面积 ,角 的平分线 交 于 , , ,则 .
16. 在△ 中,内角 的对边分别为 ,若其面积 ,角 的平分线 交 于 , , ,则 .三、解答题
-
17. 已知数列 的通项公式为 .(1)、求证:数列 是等差数列;(2)、令 ,求数列 的前 项和 .18. 如图,在直三棱柱 中, , , .
 (1)、证明: 平面 ;(2)、求三棱锥 的体积.19. 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在 , , , , , 单位:克 中,经统计得频率分布直方图如图所示.
(1)、证明: 平面 ;(2)、求三棱锥 的体积.19. 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在 , , , , , 单位:克 中,经统计得频率分布直方图如图所示. (1)、经计算估计这组数据的中位数;(2)、现按分层抽样从质量为 , 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在 内的概率.(3)、某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
(1)、经计算估计这组数据的中位数;(2)、现按分层抽样从质量为 , 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在 内的概率.(3)、某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:A:所以芒果以10元 千克收购;
B:对质量低于250克的芒果以2元 个收购,高于或等于250克的以3元 个收购.
通过计算确定种植园选择哪种方案获利更多?
20. 已知直线 过抛物线 : 的焦点,且垂直于抛物线的对称轴, 与抛物线两交点间的距离为 .(1)、求抛物线 的方程;(2)、若点 ,过点 的直线与抛物线 相交于 , 两点,设直线 与 的斜率分别为 和 .求证: 为定值,并求出此定值.