安徽省定远重点中学2018-2019学年高二上学期文数期中考试试卷
试卷更新日期:2018-12-26 类型:期中考试
一、单选题
-
1. 设命题 :“ , ”,则 为( )A、
 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  2. 已知命题 :函数 的图象恒过定点 ;命题 :若函数 为偶函数,则函数 的图象关于直线 对称,则下列命题为真命题的是( )A、
2. 已知命题 :函数 的图象恒过定点 ;命题 :若函数 为偶函数,则函数 的图象关于直线 对称,则下列命题为真命题的是( )A、 B、
B、 C、
C、 D、
D、 3. 已知命题 关于 的函数 在 上是增函数,命题 函数 为减函数,若“ 且 ”为假命题,则实数 的取值范围是( )A、
3. 已知命题 关于 的函数 在 上是增函数,命题 函数 为减函数,若“ 且 ”为假命题,则实数 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 4. 已知 是椭圆 的两个焦点,经过点 的直线交椭圆于点 ,若 ,则 等于( )A、
4. 已知 是椭圆 的两个焦点,经过点 的直线交椭圆于点 ,若 ,则 等于( )A、 B、
C、
B、
C、 D、
D、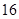 5. 设 、 分别是双曲线 的左、右焦点,点 在双曲线上,且 ,则 ( )A、1 B、3 C、3或7 D、1或96. 已知抛物线 的焦点 与双曲线 的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且 , 则△AFK的面积为( )A、4 B、8 C、16 D、327. 抛物线 的焦点为F,点 为该抛物线上的动点,又点 则 的最小值是( )A、
5. 设 、 分别是双曲线 的左、右焦点,点 在双曲线上,且 ,则 ( )A、1 B、3 C、3或7 D、1或96. 已知抛物线 的焦点 与双曲线 的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且 , 则△AFK的面积为( )A、4 B、8 C、16 D、327. 抛物线 的焦点为F,点 为该抛物线上的动点,又点 则 的最小值是( )A、 B、
C、
D、
B、
C、
D、 8. 已知抛物线C:x2=2py(p>0),若直线y=2x,被抛物线所截弦长为4 ,则抛物线C的方程为( )A、x2=8y B、x2=4y C、x2=2y D、x2=y9. 设 为可导函数,且 ,求 的值( )A、
8. 已知抛物线C:x2=2py(p>0),若直线y=2x,被抛物线所截弦长为4 ,则抛物线C的方程为( )A、x2=8y B、x2=4y C、x2=2y D、x2=y9. 设 为可导函数,且 ,求 的值( )A、 B、
B、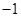 C、
D、
C、
D、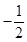 10. 已知函数 ,则 的导函数 的图象大致是( )A、
10. 已知函数 ,则 的导函数 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 11. 曲线 在点 处的切线斜率为( )A、
11. 曲线 在点 处的切线斜率为( )A、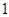 B、
B、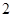 C、
C、 D、
D、 12. 设f(x)=xln x,若f′(x0)=2,则x0等于( )A、e2 B、e C、
12. 设f(x)=xln x,若f′(x0)=2,则x0等于( )A、e2 B、e C、 D、ln 2
D、ln 2
二、填空题
-
13. 若“ ”是“ ”的充分不必要条件,则实数 的取值范围是.
14. 已知命题 方程 有两个不相等的实数根;命题 关于 的函数 是 上的单调增函数,若“ 或 ”是真命题,“ 且 ”是假命题,则实数 的取值范围为 .15. 设 , 分别是双曲线 ( , )的左、右焦点,过 的直线 与双曲线分别交于 , ,且 在第一象限,若 为等边三角形,则双曲线的实轴长为 .
16. 已知函数 的导函数为 ,且 ,则 .三、解答题
-
17. 已知 ,命题 ,命题 .(1)、若p为真命题,求实数 m 的取值范围;(2)、若命题 是假命题, 命题 是真命题,求实数m的取值范围.18. 已知椭圆 的左、右焦点分别为 ,离心率为 ,点 在椭圆 上,且 的面积的最大值为 .(1)、求椭圆 的方程;(2)、已知直线 与椭圆 交于不同的两点 ,若在 轴上存在点 ,使得 ,求点 的横坐标的取值范围.19. 设 分别为双曲线 的左、右顶点,双曲线的实轴长为 ,焦点到渐近线的距离为 .(1)、求双曲线的方程;(2)、已知直线 与双曲线的右支交于 两点,且在双曲线的右支上存在点 ,使 ,求 的值及点 的坐标.
