湖北省武汉市东湖高新区2017-2018学年七年级上学期数学期中考试试卷
试卷更新日期:2018-12-24 类型:期中考试
一、单选题
-
1. 如果水位升高5m时水位记作+5m,水位不升不降时水位记作0m,那么水位下降3m时水位变化记作( )A、+3m B、﹣3m C、±3m D、﹣ m2. 把(+5)﹣(+3)+(﹣2)﹣(﹣7)写成省略括号的形式是( )A、﹣5+3+7﹣2 B、5﹣3﹣2﹣7 C、5﹣3﹣2+7 D、5+3﹣2﹣73. 超市里一袋食盐的净含量是(500±5)g,表示这袋食盐的重量范围在495g~505g之间,如果某种药品的保存温度为(20±2)℃,那么下列温度符合保存要求的是( )A、+2℃ B、﹣2℃ C、21℃ D、17℃4. 下列各组单项式中,是同类项的是( )A、 xyz与 xy B、
 与2x
C、﹣0.5x2y3与3x3y2
D、6m2n与﹣2nm2
5. 十九大报告指出:十八大以来的五年,我国国内生产总值从2012年的540000亿元增长到2016年的800000亿元,这里的800000亿元用科学记数法表示为( )A、8×105元 B、0.8×1014元 C、8×1013元 D、80×1012元6. 下列说法中,正确的是( )A、
与2x
C、﹣0.5x2y3与3x3y2
D、6m2n与﹣2nm2
5. 十九大报告指出:十八大以来的五年,我国国内生产总值从2012年的540000亿元增长到2016年的800000亿元,这里的800000亿元用科学记数法表示为( )A、8×105元 B、0.8×1014元 C、8×1013元 D、80×1012元6. 下列说法中,正确的是( )A、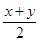 是单项式
B、﹣5不是单项式
C、﹣πx2的系数为﹣1
D、﹣πx2的次数为2
7. 下列各组等式中,正确的是( )A、﹣22=(﹣2)2 B、﹣23=(﹣2)3 C、22=﹣(﹣2)2 D、
是单项式
B、﹣5不是单项式
C、﹣πx2的系数为﹣1
D、﹣πx2的次数为2
7. 下列各组等式中,正确的是( )A、﹣22=(﹣2)2 B、﹣23=(﹣2)3 C、22=﹣(﹣2)2 D、 8. 如果 是关于 的方程 的解,那么 的值为( )A、3 B、 C、
8. 如果 是关于 的方程 的解,那么 的值为( )A、3 B、 C、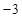 D、
9. 下列各组等式变形中,不一定成立的是( )A、如果x=y,那么
D、
9. 下列各组等式变形中,不一定成立的是( )A、如果x=y,那么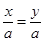 B、如果x=y,那么a+bx=a+by
C、如果
B、如果x=y,那么a+bx=a+by
C、如果 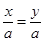 ,那么x=y
D、如果x=y,那么
,那么x=y
D、如果x=y,那么 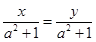 10. 下列说法中,正确的个数是( )
10. 下列说法中,正确的个数是( )①两个三次多项式的和一定是三次多项式;②如果a+b+c=0且|a|>|b|>|c|,那么ac<0;③若b是大于﹣1的负数,则b3>b2>b;④如果xyz>0,那么 的值为7或﹣1.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买3个篮球、5个排球、2个足球一共需要元.12. 某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元,如果购买甲、乙两种奖品共花费了650元,设购买了甲种奖品x件,依题意列方程得 .13. 如果方程ax|a﹣1|+3=4是关于x的一元一次方程,则a的值为 .14. 如果a>0,b<0,a+b<0,那么a,b,﹣b,﹣a大小关系是 .15. 观察下列等式: , , ,以上三个等式两边分别相加得: ,通过观察,用你发现的规律计算 = .
三、解答题
-
16.(1)、 ;(2)、 .17. 化简:(1)、7ab﹣3a2b2+7+8ab2+3a2b2﹣3﹣7ab;(2)、(4x2y﹣5xy2)﹣2(3x2y﹣4xy2)18. 有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)、这8筐白菜中最接近标准重量的这筐白菜重千克;(2)、这8筐白菜一共重多少千克?19. 先化简,再求值:,其中(2x+4)2+|4﹣6y|=0.
20. 数轴上A、B、C三点对应的数分别是a、b、c,若ab<0,c为最大的负整数,c>a且|b|>|a|. (1)、请在数轴上标出A,B,C三点的大致位置;(2)、化简|a﹣b|+|b﹣a+c|﹣|b﹣c|.21. 有一张边长为a厘米的大的正方形纸片,在它的四个角上各减去一个边长为x厘米的小正方形,折成一个无盖的长方体(如图).
(1)、请在数轴上标出A,B,C三点的大致位置;(2)、化简|a﹣b|+|b﹣a+c|﹣|b﹣c|.21. 有一张边长为a厘米的大的正方形纸片,在它的四个角上各减去一个边长为x厘米的小正方形,折成一个无盖的长方体(如图).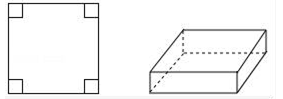 (1)、当a=9厘米时,请用含x的式子表示这个无盖长方体的体积.(2)、在(1)的条件下,当x=3厘米时求无盖长方体的体积;(3)、当a=12厘米时,要将这张正方形纸片折成一个无盖的正方体,求此时正方体的体积.22. 通过学习绝对值,我们知道|a|的几何意义是数轴上表示数a在数轴上的对应点与原点的距离,如:|5|表示5在数轴上的对应点到原点的距离.|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离,类似的,|5+3|=|5﹣(﹣3)|,即|5+3|表示5、﹣3在数轴上对应的两点之间的距离;一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为AB=|a﹣b|.
(1)、当a=9厘米时,请用含x的式子表示这个无盖长方体的体积.(2)、在(1)的条件下,当x=3厘米时求无盖长方体的体积;(3)、当a=12厘米时,要将这张正方形纸片折成一个无盖的正方体,求此时正方体的体积.22. 通过学习绝对值,我们知道|a|的几何意义是数轴上表示数a在数轴上的对应点与原点的距离,如:|5|表示5在数轴上的对应点到原点的距离.|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离,类似的,|5+3|=|5﹣(﹣3)|,即|5+3|表示5、﹣3在数轴上对应的两点之间的距离;一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为AB=|a﹣b|.请根据绝对值的几何意义并结合数轴解答下列问题:
(1)、数轴上表示2和4的两点之间的距离是;数轴上P、Q两点的距离为3,点P表示的数是4,则点Q表示的数是 .(2)、点A、B、C在数轴上分别表示数x、﹣1、2,那么A到点B、点C的距离之和可表示为(用含绝对值的式子表示);若A到点B、点C的距离之和有最小值,则x的取值范围是 .(3)、试求|x﹣1|+|x﹣2|+|x﹣3|+|x﹣4|的最小值.23. 已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点. (1)、a= , b=;并在数轴上画出A、B两点;(2)、若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;(3)、数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.
(1)、a= , b=;并在数轴上画出A、B两点;(2)、若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;(3)、数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.