重庆市江北区联盟校2018届九年级上学期数学期中考试试卷

试卷更新日期：2018-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 4的倒数是（）

A、 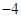B、4 C、 D、 $\frac{1}{4}$

查看试题解析
2. 下列交通指示标识中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列方程中，是关于x的一元二次方程为（）

A、x²﹣4x+5=0 B、x²+x+1=y C、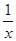 +8x﹣5=0 D、（x﹣1）²+y²=3

查看试题解析
4. 抛物线y=﹣（x+1）²﹣2的顶点坐标是（）

A、（1，2） B、（1，﹣2） C、（﹣1，2） D、（﹣1，﹣2）

查看试题解析
5. 若一元二次方程x²+2x+a=0的有实数解，则a的取值范围是（）

A、a＜1 B、a≤4 C、a≤1 D、a≥1

查看试题解析
6. 某商品原价200元，连续两次降价a%后售价为148元，下列所列方程正确的是（）

A、200（1+a%）²=148 B、200（1﹣a%）²=148 C、200（1﹣2a%）=148 D、200（1﹣a²%）=148

查看试题解析
7. 函数 $y = \frac{\sqrt{2 - x}}{x - 3}$ 的自变量x的取值范围是（）

A、x≤2 B、x≥2且x≠3 C、x≥2 D、x≤2且x≠3

查看试题解析
8. 在同一平面直角坐标系中，函数y＝ax²＋bx与y＝bx＋a的图像可能是（）

A、 B、 C、 D、

查看试题解析
9. 定义：如果一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 满足 $a + b + c = 0$ ，那么我们称这个方程为“凤凰”方程.已知 $a x^{2} + b x + c = 0 (a \neq 0)$ 是“凤凰”方程，且有两个相等的实数根，则下列结论正确的是（）

A、 B、 $a = b$ C、 D、

查看试题解析
10. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是（）

A、43 B、45 C、51 D、53

查看试题解析
11. 如图，是二次函数y=ax²+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c=0；②b＞2a；③ax²+bx+c=0的两根分别为﹣3和1；④a﹣2b+c＞0．其中正确的命题是（）

A、①② B、②③ C、①③ D、①②③④

查看试题解析
12. 如图，▱ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（）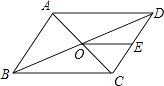

A、15 B、18 C、21 D、24

查看试题解析

二、填空题

13. “渝新欧”国际铁路联运大通道全长11000千米，成为服务“一带一路”的大动脉之一，将数11000用科学记数法表示为．

查看试题解析
14. 计算：|﹣3|+（﹣1）²﹣ $\sqrt[3]{- 8}$ = ．

查看试题解析
15. 若函数y=x²﹣6x+m的图象与x轴只有一个公共点，则m= ．

查看试题解析
16. 甲、乙两人分别从两地同时出发登山，甲、乙两人距山脚的竖直高度y（米）与登山时间x（分）之间的图象如图所示，若甲的速度一直保持不变，乙出发2分钟后加速登山，且速度是甲速度的4倍，那么他们出发分钟时，乙追上了甲．

查看试题解析
17. 如图，正方形ABCD的边长为，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为点F，则EF的长是。

查看试题解析

三、解答题

18. 解方程：

(1)、x²﹣2x=5

(2)、2（x﹣3）=3x（x﹣3）

查看试题解析
19. 如图，AB∥CD，BD=CD，∠D=36°，求∠ABC的度数．

查看试题解析
20. 2016年9月，某手机公司发布了新款智能手机，为了调查某小区业主对该款手机的购买意向，该公司在某小区随机对部分业主进行了问卷调查，规定每人只能从A类（立刻去抢购）、B类（降价后再去买）、C类（犹豫中）、D类（肯定不买）这四类中选一类，并制成了以下两幅不完整的统计图，由图中所给出的信息解答下列问题：

(1)、扇形统计图中B类对应的百分比为%，请补全条形统计图；

(2)、若该小区共有4000人，请你估计该小区大约有多少人立刻去抢购该款手机．

查看试题解析
21. 如图，在矩形ABCD中，AB=8，BC=10，E是AB上一点，将矩形ABCD沿CE折叠后，点B落在AD边的点F上，求DF的长为多少？

查看试题解析
22. 如图所示，学校准备在教学楼后面搭建一个简易矩形自行车车棚，一边利用教学楼的后墙（可利用的墙长为19m），另外三边利用学校现有总长38m的铁栏围成．

(1)、若围成的面积为180m² ，试求出自行车车棚的长和宽；

(2)、能围成的面积为200m²自行车车棚吗？如果能，请你给出设计方案；如果不能，请说明理由．

查看试题解析
23. 设a、b是任意两个实数，规定a与b之间的一种运算“⊕”为：a⊕b＝ ${\begin{matrix} \frac{b}{a} (a > 0) \\ a - b (a \leq 0) \end{matrix}$ ，例如：1⊕(－3)＝ $\frac{- 3}{1}$ ＝－3，(－3)⊕2＝(－3)－2＝－5，(x²＋1)⊕(x－1)＝ $\frac{x - 1}{x^{2} + 1}$ (因为x²＋1＞0)．参照上面材料，解答下列问题：

(1)、2⊕4＝， (－2)⊕4＝；

(2)、若x＞ $\frac{1}{2}$ ，且满足(2x－1)⊕(4x²－1)＝(－4)⊕(1－4x)，求x的值．

查看试题解析
24. 某商店经销一种成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克．若销售价每涨1元，则月销售量减少10千克．

(1)、要使月销售利润达到最大，销售单价应定为多少元？

(2)、要使月销售利润不低于8000元，请画出草图结合图象说明销售单价应如何定？

查看试题解析
25. 如图，抛物线y=ax²+bx+c（a≠0）的顶点坐标为（2，﹣1），图象与y轴交于点C（0，3），与x轴交于A、B两点．

(1)、求抛物线的解析式；

(2)、设抛物线对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；

(3)、点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．

查看试题解析