湖北省武汉市武昌区2018届九年级上学期数学期中考试试卷
试卷更新日期：2018-12-24 类型：期中考试
一、单选题
-
1. 下列图形是中心对称图形的是（ ）A、
B、
C、
D、
2. 一元二次方程x2+x﹣1=0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 方程2x2+4x﹣6=0两根之积等于（ ）A、3 B、﹣6 C、6 D、﹣34. 抛物线y=2（x﹣3）2+1的顶点坐标是（ ）A、（3，1） B、（3，﹣1） C、（﹣3，1） D、（﹣3，﹣1）5. 如图，在平面直角坐标系中，点B，C，E在y轴上，Rt△ABC经过变换得到Rt△ODE，若点C的坐标为(0，1)，AC=2，则这种变换可以是（ ）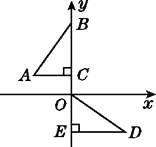
A、△ABC绕点C顺时针旋转90°，再向下平移3个单位长度 B、△ABC绕点C顺时针旋转90°，再向下平移1个单位长度 C、△ABC绕点C逆时针旋转90°，再向下平移1个单位长度 D、△ABC绕点C逆时针旋转90°，再向下平移3个单位长度6. 把抛物线y=﹣ x2向下平移3个单位长度再向左平移2个单位长度的解析式为（ ）A、 y=﹣ （x+2）2+3 B、 y=﹣ （x+2）2﹣3 C、 y=﹣ （x+3）2﹣2 D、 y=﹣ （x﹣3）2+27. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（ ）
A、30° B、40° C、50° D、65°8. 若二次函数y=x2+bx+c的图象的对称轴是经过点（2，0）且平行于y轴的直线，且过点（5，5），则关于x的方程x2+bx+c=5的解为（ ）A、x1=0或x2=4 B、x1=1或x2=5 C、x1=﹣1或 x2=5 D、x1=1或x2=﹣59. 要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场，根据时间和场地等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ）A、 x(x+1)=28 B、 x(x-1)=28 C、x(x+1)=28 D、x(x-1)=28二、填空题
-
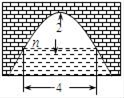
10. 方程x2﹣3x+1=0的二次项系数是；一次项系数是；常数项是 ．11. 若a2﹣3b=5，则6b﹣2a2= ．12. 函数y=x2﹣x+1的图象与y轴的交点坐标是 ．13. 有一人患了流感，经过两轮传染后共有64人患了流感，按照这样的速度，平均每人传染人．14. 如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，则水面下降1m时，水面宽度增加m．
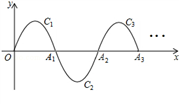
15. 如图，一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1 ， 它与x轴交于点O，A1；将C1绕点A1旋转180°得C2 ， 交x轴于点A2；
将C2绕点A2旋转180°得C3 ， 交x轴于点A3；
…
如此进行下去，直至得C13 ． 若P（37，m）在第13段抛物线C13上，则m= ．
三、解答题
-
16. 解方程：(1)、x2+2x﹣1=0(2)、x（x+4）=3x+12．17. 如图：△ABC、△ECD都是等边三角形，且B、C、D在同一直线上．
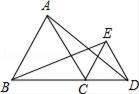(1)、求证：BE=AD；(2)、△EBC可以看做是△DAC经过平移、轴对称或旋转得到，请说明得到△EBC的过程．18. 已知关于x的一元二次方程（x-3）（x-2）=|m|．(1)、求证：对于任意实数m，方程总有两个不等的实数根；(2)、若方程的一个根是1，求m的值及方程的另一个根．19. 如图，已知二次函数y=ax2+bx+3的图象过点A（﹣1，0），顶点坐标为（1，m）．
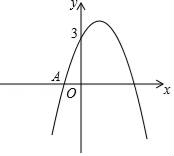(1)、求该二次函数的关系式和m值；(2)、结合图象，解答下列问题：（直接写出答案）①当x取什么值时，该函数的图象在x轴下方？
②当﹣1＜x＜2时，直接写出函数y的取值范围．
20. 如图是由边长为1的小正三角形组成的网格图，点O和△ABC的顶点都在正三角形的格点上，将△ABC绕点O逆时针旋转120°得到△A′B′C′．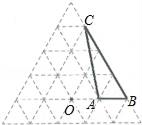
(1)、在网格中画出旋转后的△A′B′C′；(2)、以O为原点AB所在直线为x轴建立坐标系直接写出A′、B′、C′三点的坐标．21. 某网店打出促销广告：最潮新款服装30件，每件售价300元．若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，所买的每件服装的售价均降低3元．已知该服装成本是每件200元，设顾客一次性购买服装x件时，该网店从中获利y元．(1)、求y与x的函数关系式，并写出自变量x的取值范围；(2)、顾客一次性购买多少件时，该网店从中获利最多？22. 如图1，在平面直角坐标系中，抛物线C1：y=ax2+bx﹣a2关于y轴对称且有最小值﹣1．
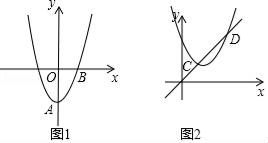(1)、求抛物线C1的解析式；(2)、在图1中抛物线C1顶点为A，将抛物线C1绕点B旋转180°后得到抛物线C2 ， 直线y=kx﹣2k+4总经过一定点M，若过定点M的直线与抛物线C2只有一个公共点，求直线l的解析式．(3)、如图2，先将抛物线 C1向上平移使其顶点在原点O，再将其顶点沿直线y=x平移得到抛物线C3 ， 设抛物线C3与直线y=x交于C、D两点，求线段CD的长．