河南省平顶山九中2018届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-24 类型:期中考试
一、单选题
-
1. 顺次连接菱形各边中点所得的四边形一定是( )A、等腰梯形 B、正方形 C、平行四边形 D、矩形2. 若x=2关于x的一元二次方程x2﹣ax+2=0的一个根,则a的值为( )A、3 B、﹣3 C、1 D、﹣13. 用频率估计概率,可以发现,某种幼树在一定条件下移植成活的概率为0.9,下列说法正确的是( )A、种植10棵幼树,结果一定是“有9棵幼树成活” B、种植100棵幼树,结果一定是“90棵幼树成活”和“10棵幼树不成活” C、种植10n棵幼树,恰好有“n棵幼树不成活” D、种植n棵幼树,当n越来越大时,种植成活幼树的频率会越来越稳定于0.94. 如图,在△ABC中E、F分别是AB、AC上的点,EF∥BC,且 ,若△AEF的面积为2,则四边形EBCF的面积为( )
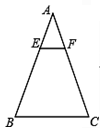 A、4 B、6 C、16 D、185. 如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
A、4 B、6 C、16 D、185. 如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )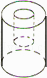 A、
A、 B、
B、 C、
C、 D、
D、 6. 某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为( ).A、5. 3米 B、4.8米 C、4.0米 D、2.7米7. 若双曲线y= 位于第二、四象限,则k的取值范围是( )A、k<1 B、k≥1 C、k>1 D、k≠18. 张华去参加聚会,每两人互相赠送礼物,他发现共送礼物20件,若设有 人参加聚会,根据题意列出方程为( )A、
6. 某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为( ).A、5. 3米 B、4.8米 C、4.0米 D、2.7米7. 若双曲线y= 位于第二、四象限,则k的取值范围是( )A、k<1 B、k≥1 C、k>1 D、k≠18. 张华去参加聚会,每两人互相赠送礼物,他发现共送礼物20件,若设有 人参加聚会,根据题意列出方程为( )A、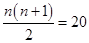 B、
B、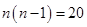 C、
C、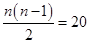 D、
D、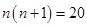 9. 如图所示,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上任意一点,则PK+QK的最小值为( )
9. 如图所示,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上任意一点,则PK+QK的最小值为( )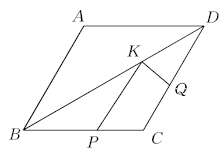 A、1 B、 C、2 D、 +1
A、1 B、 C、2 D、 +1二、填空题
-
10. 已知关于x的方程kx2﹣4x+2=0有两个实数根,则k的取值范围是 .11. 若 = = ,则 = .12. 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是 .
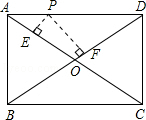 13. 如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积为(结果保留π)
13. 如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积为(结果保留π)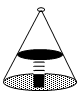 14. 如图,反比例函数y= 的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于个面积单位.
14. 如图,反比例函数y= 的图象与直线y=kx(k>0)相交于A、B两点,AC∥y轴,BC∥x轴,则△ABC的面积等于个面积单位.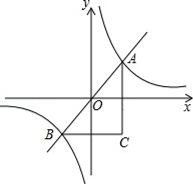
三、解答题
-
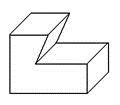
15. 画右边几何体的三种视图(注意符合三视图原则)
 16. 解方程:(1)、x2﹣4x﹣5=0(2)、x2﹣5x+1=0.17. 如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
16. 解方程:(1)、x2﹣4x﹣5=0(2)、x2﹣5x+1=0.17. 如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).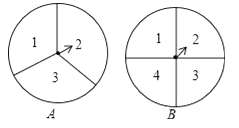 (1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.18. “泥兴陶,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:(1)、每只杯应降价多少元?(2)、在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?19. 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.18. “泥兴陶,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:(1)、每只杯应降价多少元?(2)、在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?19. 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm. (1)、求证:△AEH∽△ABC;(2)、求这个正方形的边长与面积.20. 如图,已知反比例函数 与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).
(1)、求证:△AEH∽△ABC;(2)、求这个正方形的边长与面积.20. 如图,已知反比例函数 与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4).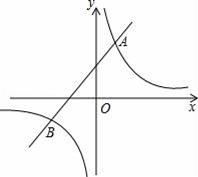 (1)、试确定这两个函数的表达式;(2)、求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.21. 如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)、试确定这两个函数的表达式;(2)、求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.21. 如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G. (1)、若FD=2, ,求线段DC的长;(2)、求证:EF·GB=BF·GE.22. 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒
(1)、若FD=2, ,求线段DC的长;(2)、求证:EF·GB=BF·GE.22. 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒 (1)、当t = 4时,求线段PQ的长度(2)、当t为何值时,△PCQ是等腰三角形?(3)、当t为何值时,△PCQ的面积等于16cm2?(4)、当t为何值时,△PCQ∽△ACB
(1)、当t = 4时,求线段PQ的长度(2)、当t为何值时,△PCQ是等腰三角形?(3)、当t为何值时,△PCQ的面积等于16cm2?(4)、当t为何值时,△PCQ∽△ACB