新人教版数新人教版数学八年级上册第十一章三角形11.3.2《多边形内角和》同步练习

试卷更新日期：2015-09-29 类型：同步测试

进入 出卷网 下载

一、选择题（共15题）

  • 1. 九边形的内角和为（　　）
    A、1260° B、1440° C、1620° D、1800°

    查看试题解析

  • 2. 一个多边形的内角和为720°，那么这个多边形的对角线共有(　　)
    A、6条 B、7条 C、8条 D、9条

    查看试题解析

  • 3. 如图，在四边形ABCD中，∠1，∠2分别是∠BCD和∠BAD的邻补角，且∠B＋∠ADC＝140°，则∠1＋∠2等于（　　）．

    A、140° B、40° C、260° D、不能确定

    查看试题解析

  • 4. 下列说法：

    ①四边形中四个内角可以都是锐角；

    ②四边形中四个内角可以都是钝角；

    ③四边形中四个内角可以都是直角；

    ④四边形中四个内角最多可以有两个钝角；

    ⑤四边形中最多可以有两个锐角.

    其中正确的是（ 　　 ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 5. 过多边形的一个顶点可以引9条对角线，那么这个多边形的内角和为（　 ）
    A、1620° B、1800° C、1980° D、2160°

    查看试题解析

  • 6. 一个多边形的每一个外角都等于且小于45°，那么这个多边形的边数最少是（　 ）
    A、7条 B、8条 C、9条 D、10条

    查看试题解析

  • 7. 如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=70°，则∠AED的度数是（　　）

    A、80° B、100° C、108° D、110°

    查看试题解析

  • 8. 一个正多边形的外角与它相邻的内角之比为1：4，那么这个多边形的边数为（　　）
    A、8 B、9 C、10 D、12

    查看试题解析

  • 9. 如图，小明将几块六边形纸片分别减掉了一部分（虚线部分），得到了一个新多边形．若新多边形的内角和为540°，则对应的是下列哪个图形（　　）
    A、 B、 C、 D、

    查看试题解析

  • 10.

    如图，平面上有两个全等的正八边形，∠BAC为（　　）


    A、60° B、45° C、30° D、72°

    查看试题解析

  • 11. 如图，在五边形ABCDE中，∠A+∠B+∠E=∠EDC+∠BCD+140°，DF，CF分别平分∠EDC和∠BCD，则∠F的度数为（　　）

    A、100° B、90° C、80° D、70°

    查看试题解析

  • 12.

    如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的对角线条数为（　　）


    A、77 B、90 C、65 D、104

    查看试题解析

  • 13. 将一个n边形变成n+1边形，内角和将（　　）
    A、减少180° B、增加90° C、增加180° D、增加360°

    查看试题解析

  • 14. 把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合，按照如图的方式叠合在一起，连接EB，交HI于点K，则∠BKI的大小为（　　）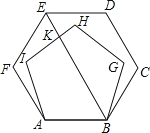

    A、90° B、84° C、72° D、88°

    查看试题解析

  • 15. 一个正方形和两个等边三角形的位置如图所示，若∠3=60°，则∠1+∠2=（　　）

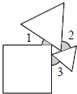    A、80° B、90° C、120° D、180°

    查看试题解析

二、填空题（共5题）

  • 16. 一个多边形每个外角都是60°，这个多边形是边形，它的内角和是度，外角和是度．

    查看试题解析

  • 17. 一个多边形的内角和等于1260°，则它的边数为 ．

    查看试题解析

  • 18. 若一个四边形的四个内角度数的比为3∶4∶5∶6，则这个四边形的四个内角的度数分别为 ．

    查看试题解析

  • 19.

    如图，小亮从点A出发前进10m向右转150º再前进10m，又向右转150º……这样一直走下去，他第一次回到出发点A时，一共走m.

    查看试题解析

  • 20.

    如图，已知四边形ABCD中，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，则∠1+∠2=°．

    查看试题解析

三、解答题（共5题）

  • 21. 一个多边形除了一个内角之外，其余内角之和为2670°，求这个多边形的边数和少加的内角的大小．

    查看试题解析

  • 22. 若多边形所有内角与它的一个外角的和为600°，求这个多边形的边数及内角和．

    查看试题解析

  • 23. 小华从点A出发向前走10m，向右转36°然后继续向前走10m，再向右转36°，他以同样的方法继续走下去，他能回到点A吗？若能，当他走回到点A时共走多少米？若不能，写出理由.

    查看试题解析

  • 24.

    求解：已知：如图1，P为△ADC内一点，DP、CP分别平分DP、CP分别平分∠ADC和∠ACD。


    (1)、如果∠A=60°，那么∠P是多少度；如果∠A=90°，那么∠P是多少度；如果∠A=x°，则∠P是多少度？

    (2)、如图2，P为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，试探究∠P与∠A+∠B的数量关系，并写出你的探索过程；

    (3)、如图3，P为五边形ABCDE内一点，DP、CP分别平分DP、CP分别平分∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E的数量关系。

    (4)、如图4，P为六边形ABCDEF内一点，DP、CP分别平分DP、CP分别平分∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E+∠F的数量关系。

    (5)、若P为n边形A1A2A3…An内一点，PA1平分∠AnA1A2 ， PA2平分∠A1A2A3 ， 请直接写出∠P与∠A3+A4+A5+…∠An的数量关系。（用含n的代数式表示）


    查看试题解析