备考2019年高考数学一轮专题:第20讲 两角和与差的正弦、余弦和正切公式
试卷更新日期:2018-12-22 类型:一轮复习
一、单选题
-
1. 计算sin43°cos13°﹣cos43°sin13°的结果等于( )A、 B、 C、 D、2. ( )
A、- B、- C、 D、3. 已知 , , ,则 ( )A、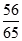 B、
B、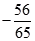 C、
C、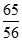 D、
D、 4. ( )A、 B、 C、 D、15. 如图所示,为测一树的高度,在地面上选取 两点,从 两点分别测得树尖的仰角为 , ,且 两点间的距离为 ,则树的高度为( )
4. ( )A、 B、 C、 D、15. 如图所示,为测一树的高度,在地面上选取 两点,从 两点分别测得树尖的仰角为 , ,且 两点间的距离为 ,则树的高度为( ) A、 B、 C、 D、6. 已知 ,则 ( )A、 B、 C、 D、7. 已知 , 则的值为 ( )A、 B、1 C、 D、28. 若在 中, ,则此三角形的形状是( )
A、 B、 C、 D、6. 已知 ,则 ( )A、 B、 C、 D、7. 已知 , 则的值为 ( )A、 B、1 C、 D、28. 若在 中, ,则此三角形的形状是( )
A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰直角三角形9. 已知 ,则 ( )A、 B、 C、 D、10. ( )A、 B、 C、 D、11. 若 ,则 ( )A、 B、 C、 D、12. ( )A、 B、 C、 D、二、填空题
-
13. (1+tan15°)(1+tan30°)=.14. 已知 , ,则 = .
15. 若 , ,则 .16. 若 ,则 的值为.三、解答题
-
17. 已知(1)、求 的值;(2)、求 的值.18. 在 中,内角 所对的边分别为 ,已知 .(1)、求角 的大小;(2)、若 ,求 的值.19. 已知函数 .(1)、求函数 图象的对称中心;(2)、求函数 的单调递减区间.20. 在 中, 分别为角 的对边,已知 , 的面积为 ,又 .(1)、求角 的大小;(2)、求 的值.21. 已知函数 的部分图象如图所示.
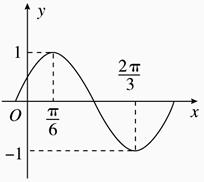 (1)、求函数 的单调递减区间;(2)、已知△ABC的内角分别是A、B、C,其中A为锐角,且 ,cosB= ,
(1)、求函数 的单调递减区间;(2)、已知△ABC的内角分别是A、B、C,其中A为锐角,且 ,cosB= ,求sinC的值.