福建福鼎三校联考2018-2019学年高三上半期文数联考试卷
试卷更新日期:2018-12-21 类型:期中考试
一、单选题
-
1. 设 ,则P是Q成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件2. 若 ,则下列不等式:① ;② ;③ ;④ 中,不正确的不等式是( )A、①④ B、②③ C、①③ D、②④3. 若向量 , 满足 , , ,则 与 的夹角为A、
 B、
B、 C、
C、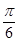 D、
D、 4. 等比数列 的各项均为正数,且 ,则A、12 B、10 C、8 D、
4. 等比数列 的各项均为正数,且 ,则A、12 B、10 C、8 D、 5. 已知函数 的部分图象如图所示,则( )
5. 已知函数 的部分图象如图所示,则( ) A、
A、 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  6. 如图,一座建筑物AB的高为 (30-10 )m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为 ( )
6. 如图,一座建筑物AB的高为 (30-10 )m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面上点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别是15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为 ( ) A、30 m B、60 m C、30 m D、40 m7. 某几何体的三视图如图所示,则该几何体的体积为( )
A、30 m B、60 m C、30 m D、40 m7. 某几何体的三视图如图所示,则该几何体的体积为( )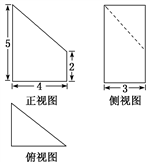 A、12 B、18 C、24 D、308. 将函数 的图象向右平移 个单位长度,所得函数图象关于 轴对称,则 的最小值为( )A、
A、12 B、18 C、24 D、308. 将函数 的图象向右平移 个单位长度,所得函数图象关于 轴对称,则 的最小值为( )A、 B、
C、
B、
C、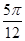 D、
D、 9. 函数f(x)= 的部分图象大致是( )A、
9. 函数f(x)= 的部分图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 数列的通项公式 , 其前项和为 , 则等于( )A、1006 B、2012 C、503 D、011. 已知正数a,b,c满足4a-2b+25c=0,则lga+lgc-2lgb的最大值为( )A、-2 B、2 C、-1 D、112. 已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2 , 对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )A、[ ,+∞) B、[2,+∞) C、(0, ] D、[0, ]
10. 数列的通项公式 , 其前项和为 , 则等于( )A、1006 B、2012 C、503 D、011. 已知正数a,b,c满足4a-2b+25c=0,则lga+lgc-2lgb的最大值为( )A、-2 B、2 C、-1 D、112. 已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2 , 对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )A、[ ,+∞) B、[2,+∞) C、(0, ] D、[0, ]二、填空题
-
13. 已知非空集合M满足:若 ,则 .则当 时,集合M的所有元素之积为 .14. 若数列 的首项 ,且 ;令 ,则 .15. 《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖,周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能装多少斛米.”则该圆柱形容器能装米斛.(古制1丈=10尺,1斛=1.62立方尺,圆周率 )16. 函数 , ,若函数 ,且函数 的零点均在 内,则 的最小值为 .
三、解答题
-
17. 在△ABC中,A、B、C所对的边分别是a、b、c,且有bcosC+ccosB=2acosB.(1)、求B的大小;(2)、若△ABC的面积是 ,且a+c=5,求b.18. 已知函数 的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列 的前n项和Sn=f(n)(n∈N*).(1)、求数列 的通项公式;(2)、求数列{ }前n项的和Tn .19. 如图在三棱锥 中, 分别为棱 的中点,已知 ,

求证:
(1)、直线 平面 ;(2)、平面 平面 .20. 某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当 的学生选择自行打车,自行打车的平均时间为 (单位:分钟) ,而乘坐定制公交的平均时间不受 影响,恒为40分钟,试根据上述分析结果回答下列问题:(1)、当 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?(2)、求该校学生参加考试平均时间 的表达式:讨论 的单调性,并说明其实际意义.