安徽皖东名校联盟2018-2019学年高三上学期文数第二次联考试卷
试卷更新日期:2018-12-21 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 的真子集有( )A、1个 B、2个 C、3个 D、4个2. 设 是虚数单位,条件 复数 是纯虚数,条件 ,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 函数 的定义域是( )A、 B、
 C、
C、 D、
D、 4. 函数 ( )A、没有零点 B、有一个零点 C、有两个零点 D、有一个零点或有两个零点5. 函数 在 内( )A、单调递增 B、单调递减 C、有增有减 D、无法判定6. 函数 的部分图象可能是( )A、
4. 函数 ( )A、没有零点 B、有一个零点 C、有两个零点 D、有一个零点或有两个零点5. 函数 在 内( )A、单调递增 B、单调递减 C、有增有减 D、无法判定6. 函数 的部分图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 若函数 在 上的最大值是3,则实数 ( )A、3 B、2 C、1 D、08. 若抛物线 在点 处的切线与两条坐标轴围成的三角形的面积是8,则此切线方程是( )A、
7. 若函数 在 上的最大值是3,则实数 ( )A、3 B、2 C、1 D、08. 若抛物线 在点 处的切线与两条坐标轴围成的三角形的面积是8,则此切线方程是( )A、 B、
B、 C、
C、 D、
D、 9. 设 均大于1,且 ,令 ,则 的大小关系是( )A、
9. 设 均大于1,且 ,令 ,则 的大小关系是( )A、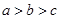 B、
B、 C、
C、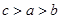 D、
D、 10. 已知定义在 上的函数 满足 ,当 时, ,则当 时, ( )A、
10. 已知定义在 上的函数 满足 ,当 时, ,则当 时, ( )A、 B、
B、 C、
C、 D、
D、 11. 下列判断中正确的是( )A、“若
11. 下列判断中正确的是( )A、“若 ,则
,则  有实数根”的逆否命题是假命题
B、“
有实数根”的逆否命题是假命题
B、“  ”是“直线
”是“直线  与直线
与直线  平行”的充要条件
C、命题“
平行”的充要条件
C、命题“  ”是真命题
D、命题“
”是真命题
D、命题“  ”在
”在  时是假命题
12. 若函数 的最大值是4,则 的取值范围是( )A、
时是假命题
12. 若函数 的最大值是4,则 的取值范围是( )A、 B、
B、 C、
C、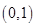 D、
D、
二、填空题
-
13. 命题“ ”的否定是 .14. 若三次函数 的导函数 的图象如图所示,则实数 的值是 .
 15. 用小于号连接 和 ,结果是 .16. 若直线 与曲线 有公共点,则实数 的最大值是 .
15. 用小于号连接 和 ,结果是 .16. 若直线 与曲线 有公共点,则实数 的最大值是 .三、解答题
-
17. 已知关于 的函数 ,其中 .
(Ⅰ)当 时,求满足 的实数 的取值范围;
(Ⅱ)若当 时,函数 的图象总在直线 的上方,求 的整数值.
18. 设 ,命题 “方程 有实数根”, 命题 “对任意实数 , 恒成立”.(1)、若 为真命题,求 的最大值;(2)、若 为真命题,且 为假命题,求 的取值范围.19. 已知函数 .(1)、当 时,求 的单调区间;(2)、若 在区间 内单调递增,求 的取值范围.20. 我们常常称恒成立不等式 ( ,当且仅当 时等号成立)为“灵魂不等式”,它在处理函数与导数问题中常常发挥重要作用.(1)、试证明这个不等式;(2)、设函数 ,且在定义域内恒有 ,求实数 的值.