浙江省湖州市2017-2018学年高一下学期数学期末考试试卷
试卷更新日期:2018-12-21 类型:期末考试
一、单选题
-
1. 直线 的倾斜角是A、
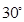 B、
B、 C、
C、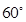 D、
D、
-
2. 在等比数列 中, , ,则公比q是A、2 B、3 C、4 D、5
-
3. 若 , ,则一定有A、
 B、
B、 C、
C、 D、
D、
-
4. 若圆 与圆 关于原点对称,则圆 的方程是A、
 B、
B、 C、
C、 D、
D、
-
5. 若关于x的不等式 的解集是 ,则不等式 的解集是A、
 B、
B、 或
或  C、
C、 D、
D、 或
或 
-
6. 已知不等式 对任意正实数x,y恒成立,则正实数m的最小值是A、2 B、4 C、6 D、8
-
7. 莱因德纸草书 是世界上最古老的数学著作之一,书中有一道这样的题目:把120个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小一份面包是A、2个 B、13个 C、24个 D、35个
-
8. 在 中,边a,b,c所对的角分别为A,B,C,若 , ,则A、
 B、
B、 C、
C、 D、
D、
-
9. 已知数列 的首项 ,前n项和为 ,且满足 ,则满足 的n的最大值是A、8 B、9 C、10 D、11
-
10. 过点 作直线 的垂线,垂足为M,已知点 ,则当 变化时, 的取值范围是A、
 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知两点 ,则直线AB的斜率k的值是 , 直线AB在y轴的截距是 .
-
12. 已知数列 的前n项和 则 .
-
13. 已知实数x,y满足 ,此不等式组表示的平面区域的面积为 , 目标函数 的最小值为 .
-
14. 已知a,b都为正实数,且 ,则ab的最小值是 , 的最大值是 .
-
15. 已知圆 与圆 相交于M,N两点,则直线MN的方程是 .
-
16. 若锐角 的面积为 , , ,则BC边上的中线AD的长是 .
-
17. 已知 ,记函数 在 的最大值为 ,则实数t的值是 .
三、解答题
-
18. 已知直线 : ,直线 : .
Ⅰ 若直线 与直线 平行,求实数a的值;
Ⅱ 若直线 与直线 垂直,求直线 与 的交点坐标.
-
19. 已知公差不为零的等差数列 的前10项和 ,且 , , 成等比数列.
Ⅰ 求数列 的通项公式;
Ⅱ 若数列 满足 ,求数列 的前n项和 .
-
20. 已知 的内角A,B,C的对边分别是a,b,c,且 .
Ⅰ 求角A的大小;
Ⅱ 若 ,求 的取值范围.
-
21. 已知圆心在x轴正半轴上的圆C与直线 相切,与y轴交于M,N两点,且 .

Ⅰ 求圆C的标准方程;
Ⅱ 过点 的直线l与圆C交于不同的两点D,E,若 时,求直线l的方程;
Ⅲ 已知Q是圆C上任意一点,问:在x轴上是否存在两定点A,B,使得 ?若存在,求出A,B两点的坐标;若不存在,请说明理由.
-
22. 已知数列 满足 ,且 .
Ⅰ 使用数学归纳法证明: ;
Ⅱ 证明: ;
Ⅲ 设数列 的前n项和为 ,证明: .
