安徽省定远重点中学2019届高三上学期文数期中考试试卷
试卷更新日期:2018-12-21 类型:期中考试
一、单选题
-
1. 已知命题 ,命题 , 若命题“ 且 ”是真命题, 则实数 的取值范围是( )A、
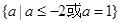 B、
B、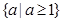 C、
C、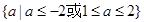 D、
D、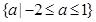 2. 设A是自然数集的一个非空子集,对于k∈A,如果k2∉A,且 ∉A,那么k是A的一个“酷元”,给定S={x∈N|y=lg(36-x2)},设M⊆S,且集合M中的两个元素都是“酷元”,那么这样的集合M有( )A、3个 B、4个 C、5个 D、6个3. 已知正三角形 的边长为 ,平面 内的动点 满足 , ,则 的最大值是( )A、
2. 设A是自然数集的一个非空子集,对于k∈A,如果k2∉A,且 ∉A,那么k是A的一个“酷元”,给定S={x∈N|y=lg(36-x2)},设M⊆S,且集合M中的两个元素都是“酷元”,那么这样的集合M有( )A、3个 B、4个 C、5个 D、6个3. 已知正三角形 的边长为 ,平面 内的动点 满足 , ,则 的最大值是( )A、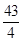 B、
B、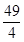 C、
C、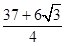 D、
D、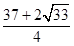 4. 设函数f(x)= ,[x]表示不超过x的最大整数,则函数y=[f(x)]的值域是 ( )A、{0,1} B、{0,-1} C、{-1,1} D、{1,1}5. 定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有( )A、最小值f(a) B、最大值f(b) C、最小值f(b) D、最大值f
4. 设函数f(x)= ,[x]表示不超过x的最大整数,则函数y=[f(x)]的值域是 ( )A、{0,1} B、{0,-1} C、{-1,1} D、{1,1}5. 定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有( )A、最小值f(a) B、最大值f(b) C、最小值f(b) D、最大值f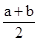 6. 已知 是R上的单调递增函数,则实数
6. 已知 是R上的单调递增函数,则实数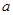 的取值范围为 ( ) A、(1,+∞) B、[4,8) C、(4,8) D、(1,8)7. 函数 的图象的大致形状是( )A、
的取值范围为 ( ) A、(1,+∞) B、[4,8) C、(4,8) D、(1,8)7. 函数 的图象的大致形状是( )A、 B、
B、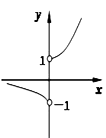 C、
C、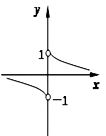 D、
D、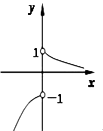 8. 已知{an}是公差为1的等差数列;Sn为{an}的前n项和,若S8=4S4 , 则a10=( )A、
8. 已知{an}是公差为1的等差数列;Sn为{an}的前n项和,若S8=4S4 , 则a10=( )A、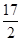 B、
B、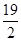 C、10
D、12
9. 设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定10. 若函数 在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a的取值范围是 ( )A、a≤2 B、5≤a≤7 C、4≤a≤6 D、a≤5或a≥711. 将函数 的图象向右平移 个单位后得到函数 的图象,若对满足 的 ,有 的最小值为 ,则 ( )A、
C、10
D、12
9. 设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定10. 若函数 在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a的取值范围是 ( )A、a≤2 B、5≤a≤7 C、4≤a≤6 D、a≤5或a≥711. 将函数 的图象向右平移 个单位后得到函数 的图象,若对满足 的 ,有 的最小值为 ,则 ( )A、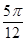 B、
B、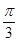 C、
C、 D、
D、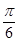 12. 已知函数 , ,则 是( )A、最小正周期为
12. 已知函数 , ,则 是( )A、最小正周期为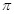 的奇函数
B、最小正周期为
的奇函数
B、最小正周期为 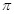 的偶函数
C、最小正周期为
的偶函数
C、最小正周期为  的奇函数
D、最小正周期为
的奇函数
D、最小正周期为  的偶函数
的偶函数
二、填空题
-
13. 已知实数 满足 ,如果目标函数 的最小值为-1,则实数 .14. 已知 =(cosθ,sinθ), =(3-cosθ,4-sinθ),若 ∥ ,则cos2θ=.15. 数列{ }的构成法则如下: =1,如果 -2为自然数且之前未出现过,则用递推公式 = -2.否则用递推公式 =3 ,则 =.16. 若 , ,则 =
三、解答题
-
17. 已知集合M={x|x<-3,或x>5},P={x|(x-a)·(x-8)≤0}.(1)、求M∩P={x|5<x≤8}的充要条件;(2)、求实数a的一个值,使它成为M∩P={x|5<x≤8}的一个充分但不必要条件.18. 已知 为 的三个内角,其所对的边分别为 ,且 .(1)、求角 的值;(2)、若 ,求 的面积.19. 已知 ,点 在函数 的图象上,其中n=1,2,3,….(1)、证明:数列 是等比数列;(2)、设 ,求 及数列 的通项;(3)、记 ,求数列{bn}的前n项和Sn,并证明Sn+ =1.