浙江省宁波市鄞州区七校2019届九年级上学期数学期中考试试卷
试卷更新日期:2018-12-21 类型:期中考试
一、精心选一
-
1. 若 ,则下列选项正确的是( )A、
 B、
B、  C、
C、  D、
D、 2. 下列成语所描述的事件,是随机事件的是( )A、水涨船高 B、一箭双雕 C、水中捞月 D、一步登天3. 抛物线 的顶点坐标( )A、
2. 下列成语所描述的事件,是随机事件的是( )A、水涨船高 B、一箭双雕 C、水中捞月 D、一步登天3. 抛物线 的顶点坐标( )A、 B、
B、 C、
C、 D、
D、 4. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( )
4. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( )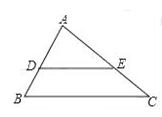 A、1 B、 C、
A、1 B、 C、 D、
D、 5. 在平面直角坐标系中,点M(2,0),⊙M的半径为4,那么点P(-2,3)与⊙M的位置关系是( )A、点P在圆内 B、点P在圆上 C、点P在圆外 D、不能确定6. 已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=﹣2x2﹣8x+m上的点,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y3<y17. 如果一个扇形的半径是1,弧长是 ,那么此扇形的圆心角的大小为( )A、30° B、45° C、60° D、90°8. 如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为6,则阴影部分的面积为( )
5. 在平面直角坐标系中,点M(2,0),⊙M的半径为4,那么点P(-2,3)与⊙M的位置关系是( )A、点P在圆内 B、点P在圆上 C、点P在圆外 D、不能确定6. 已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=﹣2x2﹣8x+m上的点,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y3<y17. 如果一个扇形的半径是1,弧长是 ,那么此扇形的圆心角的大小为( )A、30° B、45° C、60° D、90°8. 如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为6,则阴影部分的面积为( )
 A、
A、 B、6π
C、
B、6π
C、 D、
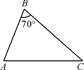
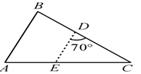
D、 9. 如图所示,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形相似的有( ).
9. 如图所示,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形相似的有( ).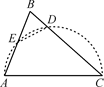
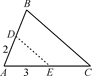
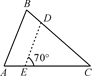 A、1个 B、2个 C、3个 D、4个10. 下列命题正确的个数为( )
A、1个 B、2个 C、3个 D、4个10. 下列命题正确的个数为( )①圆心角相等,所对的弦也相等。 ②等弧所对的弦相等 ③平分弦的直径垂直弦。④矩形都相似。 ⑤三点确定一个圆
A、1个 B、2个 C、3个 D、4个11. 如图,已知二次函数 的图像如图所示,有下列5个结论:① ,② ,③ ,④ ⑤ 。其中正确的结论有( ) A、①②③ B、①③ ④ C、③④⑤ D、②③⑤12. 如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE,AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是( )
A、①②③ B、①③ ④ C、③④⑤ D、②③⑤12. 如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE,AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MP•MD=MA•ME;③2CB2=CP•CM.其中正确的是( )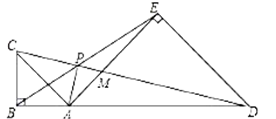 A、①②③ B、① C、①② D、②③
A、①②③ B、① C、①② D、②③二、细心填一填
-
13. 从 ,0,π,6这4个数中随机抽取一个数,抽到有理数的概率是 。14. 抛物线y=-x2向上平移2个单位,再向右平移3个单位得到图象的解析式为。15. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为
 16. 半径为2cm的⊙O中有长为 cm的弦AB,则 弦AB所对的圆周角度数为。17. 如图所示,两根竖直的电线杆AB长为6,CD长为3,AD交BC于点E,则点E到地
16. 半径为2cm的⊙O中有长为 cm的弦AB,则 弦AB所对的圆周角度数为。17. 如图所示,两根竖直的电线杆AB长为6,CD长为3,AD交BC于点E,则点E到地面的距离EF的长是 。
 18. 如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为 .
18. 如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为 .
三、用心做一做
-
19. 如图,在所给的方格纸中,每个小正方形边长都是1,△ABC是格点三角形(顶点在方格顶点处).
 (1)、在图中画格点△A1B1C1 , 使△A1B1C1与△ABC相似,相似比为2︰1.(2)、在图中画格点△A2B2C2 , 使△A2B2C2与△ABC相似,面积比为2︰1.20. 有三张分别标有数字2,5,9的卡片,它们的背面都相同.现将它们背面朝上,从中任意抽出一张卡片,不放回,再从剩余的两张卡片里任意抽出一张.(1)、请用树状图或列表法表示出所有可能的结果.(2)、求两张卡片的数字之和为偶数的概率.21. 如图,在△ABC中,AB=4cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒后,点P、B、Q构成的三角形△PBQ与△ABC相似?
(1)、在图中画格点△A1B1C1 , 使△A1B1C1与△ABC相似,相似比为2︰1.(2)、在图中画格点△A2B2C2 , 使△A2B2C2与△ABC相似,面积比为2︰1.20. 有三张分别标有数字2,5,9的卡片,它们的背面都相同.现将它们背面朝上,从中任意抽出一张卡片,不放回,再从剩余的两张卡片里任意抽出一张.(1)、请用树状图或列表法表示出所有可能的结果.(2)、求两张卡片的数字之和为偶数的概率.21. 如图,在△ABC中,AB=4cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒后,点P、B、Q构成的三角形△PBQ与△ABC相似? 22. 若直线y=x+3与二次函数y=-x2+2x+3的图象交于A,B两点,(1)、求A,B两点的坐标.(2)、求△OAB的面积.(3)、x为何值时,一次函数的值大于二次函数的值?23. 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于
22. 若直线y=x+3与二次函数y=-x2+2x+3的图象交于A,B两点,(1)、求A,B两点的坐标.(2)、求△OAB的面积.(3)、x为何值时,一次函数的值大于二次函数的值?23. 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F.
 (1)、请写出三条与BC有关的正确结论;(2)、当∠D=30°,BC=1时,求圆中阴影部分的面积.24. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)、请写出三条与BC有关的正确结论;(2)、当∠D=30°,BC=1时,求圆中阴影部分的面积.24. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)、当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(2)、为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?25. 数学课上,神奇而有魔力的黄金分割点激起了同学们的极大兴趣,某学习兴趣小组在探究该知识时,由“黄金分割点”联想到“黄金分割线”,类似地给出定义:直线AB将一个面积为S的图形分成两部分,这两部分的面积分别为S1和S2 , 如果 ( > ),那么称直线AB为该图形的黄金分割线

 (1)、该学习兴趣小组猜想:如图1,在矩形ABCD中,若点E是线段BC的黄金分割点(BE<EC),则线段BC的垂线EF就是矩形ABCD的黄金分割线,你认为对吗?为什么?(2)、该学习兴趣小组在进一步探究中发现:如图2,在(1)的条件下,点M是线段EF的中点,另外一条直线GH经过点M,则直线GH也是矩形ABCD的黄金分割线,请你说明理由(3)、请你比较分析与动手操作:
(1)、该学习兴趣小组猜想:如图1,在矩形ABCD中,若点E是线段BC的黄金分割点(BE<EC),则线段BC的垂线EF就是矩形ABCD的黄金分割线,你认为对吗?为什么?(2)、该学习兴趣小组在进一步探究中发现:如图2,在(1)的条件下,点M是线段EF的中点,另外一条直线GH经过点M,则直线GH也是矩形ABCD的黄金分割线,请你说明理由(3)、请你比较分析与动手操作:①一条线段有两个黄金分割点,一个矩形有条黄金分割线
②如图3所示,在△ABC中,点E是线段BC的黄金分割点(BE<EC),点F是线段BC上的另外一点(异于点E),请过点F作一条△ABC的黄金分割线,并说明理由
26. 如图,在等腰△ABC中,AB=AC=5cm,BC=6cm,点P从点B开始沿BC边以每秒1cm的速度向点C运动,点Q从点C开始沿CA边以每秒2 cm的速度向点A运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E. 点P,Q分别从B,C两点同时出发,当点Q运动到点A时,点Q、P停止运动,设它们运动的时间为xcm. (1)、当x=秒时,射线DE经过点C;(2)、当点Q运动时,设四边形ABPQ的面积为ycm2 , 求y与x的函数关系式(不用写出自变量取值范围);(3)、当点Q运动时,是否存在以P、Q、C为顶点的三角形与△PDE相似?若存在,求出x的值;若不存在,请说明理由。
(1)、当x=秒时,射线DE经过点C;(2)、当点Q运动时,设四边形ABPQ的面积为ycm2 , 求y与x的函数关系式(不用写出自变量取值范围);(3)、当点Q运动时,是否存在以P、Q、C为顶点的三角形与△PDE相似?若存在,求出x的值;若不存在,请说明理由。