浙江省宁波市鄞州区七校2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-12-21 类型:期中考试
一、精心选一选
-
1. 已知三角形的两边长分别为3和4,则第三边长的取值范围在数轴上表示正确的是( )A、
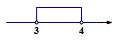 B、
B、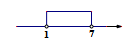 C、
C、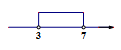 D、
D、 2. 下列图形中,轴对称图形有( )
2. 下列图形中,轴对称图形有( ) A、1个 B、2个 C、3个 D、4个3. 如果 ,下列各式中不正确的是( )A、
A、1个 B、2个 C、3个 D、4个3. 如果 ,下列各式中不正确的是( )A、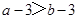 B、
B、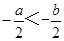 C、
C、 D、
D、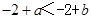 4. 点P(-2,2)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中,是真命题的是( )A、成轴对称的两个图形是全等图形 B、面积相等的两个三角形全等 C、三角形的三条高线相交于三角形内一点 D、内错角相等6. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
4. 点P(-2,2)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中,是真命题的是( )A、成轴对称的两个图形是全等图形 B、面积相等的两个三角形全等 C、三角形的三条高线相交于三角形内一点 D、内错角相等6. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( ) A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠27. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠27. 如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )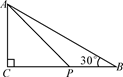 A、3.5 B、4.2 C、5.8 D、78. 如图,在△ABC中,BD=CD, AD⊥BC,垂足为D,E是AC的中点.若AB=5,则DE的长为( )
A、3.5 B、4.2 C、5.8 D、78. 如图,在△ABC中,BD=CD, AD⊥BC,垂足为D,E是AC的中点.若AB=5,则DE的长为( )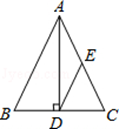 A、2 B、2.5 C、3 D、49. 如图,在长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A、2 B、2.5 C、3 D、49. 如图,在长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )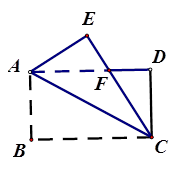 A、 B、 C、 D、10. 不等式组 的解集是 ,那么 的取值范围是( )A、
A、 B、 C、 D、10. 不等式组 的解集是 ,那么 的取值范围是( )A、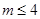 B、
B、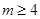 C、
C、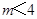 D、
D、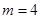
二、细心填一填
-
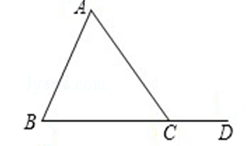
11. 如图,∠ACD是△ABC的外角,若∠ACD=125°,∠A=75°,则∠B=度.
 12. 在平面坐标系上,若点P(m,m-2)在第一象限,则m的取值范围是 .13. 已知点A(m,3)与点B(2,n)关于y轴对称,则mn=14. 在 中,AB=AC=13,BC=10,且 ⊥ 于点 ,则15. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
12. 在平面坐标系上,若点P(m,m-2)在第一象限,则m的取值范围是 .13. 已知点A(m,3)与点B(2,n)关于y轴对称,则mn=14. 在 中,AB=AC=13,BC=10,且 ⊥ 于点 ,则15. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .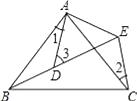 16. 命题“等腰三角形的两个底角相等.”的逆命题是 .17. 线段AB两端点A(-1,2),B(4,2),则线段AB上任意一点可表示为 .18. 如图,△ABC中∠ABC=∠ACB,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=
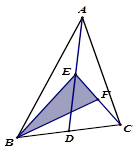
16. 命题“等腰三角形的两个底角相等.”的逆命题是 .17. 线段AB两端点A(-1,2),B(4,2),则线段AB上任意一点可表示为 .18. 如图,△ABC中∠ABC=∠ACB,AB的垂直平分线交AC于点D.若∠A=40°,则∠DBC=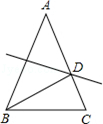 19. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2 ,
19. 如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2 ,则S阴影等于cm2
 20. 如图:长方形ABCD中,AD=26,AB=12,点Q是BC的中点,点P在AD边上运动,当△BPQ是以QP为腰的等腰三角形时,AP的长为.
20. 如图:长方形ABCD中,AD=26,AB=12,点Q是BC的中点,点P在AD边上运动,当△BPQ是以QP为腰的等腰三角形时,AP的长为.
三、用心做一做
-
21. 解下列不等式(组),并把(1)的解集在数轴上表示出来(1)、7x-2≥5x+2(2)、22. △ 在平面直角坐标系 中的位置如图所示.
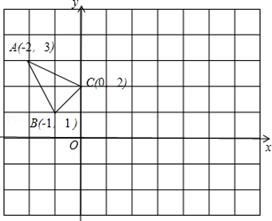 (1)、①作△ 关于y轴成轴对称的△ .
(1)、①作△ 关于y轴成轴对称的△ .②将△ 向右平移3个单位,作出平移后的△ .
(2)、在 轴上求作一点 ,使 的值最小,并求出其最小值.23. 已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,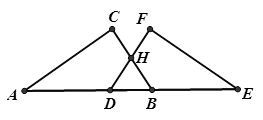 (1)、求证:△ABC≌△EDF;(2)、当∠CHD=120°,猜想△HDB的形状,并说明理由.24. 某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1 820元.(1)、求购买一套A型课桌凳和一套B型课桌凳各需多少元.(2)、学校更具实际情况,要求购买这两套课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的 ,该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?25. 如图:在△ABC中,AB=10cm,BC=6cm,AC=8cm,BD是∠ABC的角平分线。
(1)、求证:△ABC≌△EDF;(2)、当∠CHD=120°,猜想△HDB的形状,并说明理由.24. 某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1 820元.(1)、求购买一套A型课桌凳和一套B型课桌凳各需多少元.(2)、学校更具实际情况,要求购买这两套课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的 ,该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?25. 如图:在△ABC中,AB=10cm,BC=6cm,AC=8cm,BD是∠ABC的角平分线。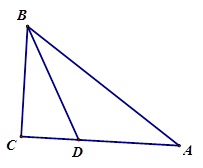 (1)、求△ABC的面积;(2)、求△ABC的角平分线BD的长;(3)、若点E是线段AB上的一个动点,从点B以每秒2cm的速度向A运动,几秒种后△EAD是直角三角形?(此小题可直接写出答案)26. 定义:如图1,等腰△ABC中,点E , F分别在腰AB , AC上,连结EF , 若AE=CF , 则称EF为该等腰三角形的逆等线.
(1)、求△ABC的面积;(2)、求△ABC的角平分线BD的长;(3)、若点E是线段AB上的一个动点,从点B以每秒2cm的速度向A运动,几秒种后△EAD是直角三角形?(此小题可直接写出答案)26. 定义:如图1,等腰△ABC中,点E , F分别在腰AB , AC上,连结EF , 若AE=CF , 则称EF为该等腰三角形的逆等线.
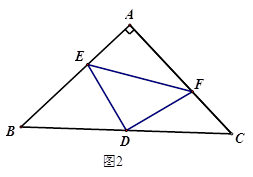
 (1)、如图1,EF是等腰△ABC的逆等线,若EF⊥AB , AB=AC=5,AE =2,求逆等线EF的长;(2)、如图2,若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点,且点E , F分别在AB , AC上,求证:EF为等腰△ABC的逆等线;(3)、如图3,边长为6的等边三角形△AOC的边OC与X轴重合,EF是该等边三角形的逆等线.F点的坐标为(5, );试求点E的坐标(若需要,本题可以直接应用结论:在直角三角形中,30°角所对的直角边等于斜边的一半.)
(1)、如图1,EF是等腰△ABC的逆等线,若EF⊥AB , AB=AC=5,AE =2,求逆等线EF的长;(2)、如图2,若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点,且点E , F分别在AB , AC上,求证:EF为等腰△ABC的逆等线;(3)、如图3,边长为6的等边三角形△AOC的边OC与X轴重合,EF是该等边三角形的逆等线.F点的坐标为(5, );试求点E的坐标(若需要,本题可以直接应用结论:在直角三角形中,30°角所对的直角边等于斜边的一半.)