江苏省南京市联合体2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2018-12-21 类型：期中考试

进入出卷网下载

一、单选题

1. 比﹣1小2的数是（）

A、3 B、1 C、﹣2 D、﹣3

查看试题解析
2. 把(－2)－(＋3)－(－5)＋(－4)统一为加法运算，正确的是（）．

A、(－2)＋(＋3)＋(－5)＋(－4) B、(－2)＋(－3)＋(＋5)＋(－4) C、(－2)＋(＋3)＋(＋5)＋(＋4) D、(－2)＋(－3)＋(－5)＋(＋4)

查看试题解析
3. 下列各组数中，数值相等的是（）．

A、(－2)³和(－3)² B、－3²和(－3)² C、－3³和(－3)³ D、－3×2³和(－3×2)³

查看试题解析
4. 下列去括号正确的是（）．

A、－2(a＋b)＝－2a＋b B、－2(a＋b)＝－2a－b C、－2(a＋b)＝－2a－2b D、－2(a＋b)＝－2a＋2b

查看试题解析
5. 下列等式变形正确的是（）．

A、如果mx＝my，那么x＝y B、如果︱x︱＝︱y︱，那么x＝y C、如果－ $\frac{1}{2}$ x＝8，那么x＝－4 D、如果x－2＝y－2，那么x＝y

查看试题解析
6. 若967×85＝p，则967×84的值可表示为（）．

A、p－967 B、p－85 C、p－1 D、 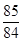p

查看试题解析
7. 图案的地砖，要求灰、白两种颜色面积大致相同，那么下面最符合要求的是（）．

A、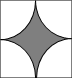 B、 C、 D、

查看试题解析
8. 四个数轴上的点A都表示数a，其中，一定满足︱a︱＞2的是（）．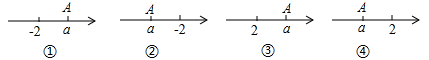

A、①③ B、②③ C、①④ D、②④

查看试题解析

二、填空题

9. - $\frac{1}{3}$ 的相反数是，绝对值是，倒数是．

查看试题解析
10. 比较大小：－2.3－2.4（填“＞”或“＜”或“＝”）．

查看试题解析
11. 单项式－4πab²的系数是，次数是．

查看试题解析
12. 研究表明，可燃冰是一种可替代石油的新型清洁能源，在我国某海域已探明的可燃冰储存量达150 000 000 000 m³ ，其中数字150 000 000 000用科学记数法可表示为．

查看试题解析
13. 数轴上将点A移动4个单位长度恰好到达原点，则点A表示的数是．

查看试题解析
14. “减去一个数，等于加上这个数的相反数”用字母可以表示为．

查看试题解析
15. 若5x⁶y^2m与－3xⁿ⁺⁹y⁶和是单项式，那么n－m的值为．

查看试题解析
16. 若a-2b=3，则2a-4b-5=.

查看试题解析
17. 一米长的木棒，第1次截去一半，第2次截去剩下的一半，……，如此截下去，第次截去后剩下的小棒长 $\frac{1}{64}$ 米．

查看试题解析
18. 若a＜0，b＞0，在a＋b，a－b，－a＋b，－a－b中最大的是．

查看试题解析

三、解答题

19. 计算：

(1)、(－8)＋10－2＋(－1)；

(2)、12－7×(－4)＋8÷(－2)；

(3)、( $\frac{1}{2} + \frac{1}{3} - \frac{1}{6}$ )÷(－ $\frac{1}{18}$ )；

(4)、－1⁴－(1＋0.5)× $\frac{1}{3}$ ÷(－4)² ．

查看试题解析
20. 化简：

(1)、3x²－2xy＋y²－3x²+3xy；

(2)、(7x²－3xy)－6(x²－ $\frac{1}{3}$ xy)．

查看试题解析
21. 先化简，再求值：5(3a²b－ab²)－(ab²+3a²b)，其中a＝－ $\frac{1}{2}$ ，b＝2．

查看试题解析
22. 解方程：

(1)、2x+1＝8－5x；

(2)、 $\frac{x + 2}{4} - \frac{2 x - 3}{6} = 1$ ．

查看试题解析
23. 某市出租车的计价标准为：行驶路程不超过3 km收费10元，超过3 km的部分按每千米1.8元收费．

(1)、某出租车行程为x km，若x＞3 km，则该出租车驾驶员收到车费元(用含有 $x$ 的代数式表示)；

(2)、一出租车公司坐落于东西向的宏运大道边，某驾驶员从公司出发，在宏运大道上连续接送4批客人，行驶路程记录如下(规定向东为正，向西为负，单位：km) ．

第1批

第2批

第3批

第4批

5

2

－4

－12

①送完第4批客人后，该出租车驾驶员在公司的边(填“东或西”)，距离公司km的位置；

查看试题解析
24. 如图，长为50 cm，宽为x cm的大长方形被分割为 $8$ 小块，除阴影A，B外，其余 $6$ 块是形状、大小完全相同的小长方形，其较短一边长为a cm．

(1)、从图可知，每个小长方形较长一边长是 cm（用含a的代数式表示）．

(2)、求图中两块阴影 $A$ ， $B$ 的周长和（可以用含x的代数式表示）．

查看试题解析
25. 定义☆运算
观察下列运算：

(＋3)☆(＋15) ＝＋18    (－14)☆(－7) ＝＋21，

(－2)☆(＋14) ＝－16    (＋15)☆(－8) ＝－23，

0☆(－15) ＝＋15       (＋13)☆0 ＝＋13．

(1)、请你认真思考上述运算，归纳☆运算的法则：
两数进行☆运算时，同号，异号．

特别地， $0$ 和任何数进行☆运算，或任何数和 $0$ 进行☆运算，．

(2)、计算：(＋11) ☆[0 ☆(－12)] ＝．

(3)、若2×(2☆a)－1＝3a，求a的值．

查看试题解析
26.

(1)、【归纳】观察下列各式的大小关系：
|－2|＋|3|＞|－2＋3| |－6|＋|3|＞|－6＋3|

|－2|＋|－3|＝|－2－3| |0|＋|－8|＝|0－8|

归纳：|a|＋|b||a＋b|（用“＞”或“＜”或“＝”或“≥”或“≤”填空）

(2)、【应用】根据上题中得出的结论，若|m|＋|n|＝13，|m＋n|＝1，求m的值．

(3)、【延伸】a、b、c满足什么条件时，|a|＋|b|＋|c|＞|a＋b＋c|．

查看试题解析

第1批	第2批	第3批	第4批
5	2	－4	－12