安徽省定远重点中学2018-2019学年高三上学期理数期中考试试卷
试卷更新日期:2018-12-21 类型:期中考试
一、单选题
-
1. 已知集合M={x| ≥0,x∈R},N={y|y=3x2+1,x∈R},则M∩N等于( )A、∅ B、{x|x≥1} C、{x|x>1} D、{x|x≥1或x<0}2. 若α∈R,则“α=0”是“sinα<cosα”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 设 的三个内角 ,向量 , ,若 ,则 =( )A、 B、 C、 D、4. 设 是公差不为0的等差数列, 且 成等比数列,则 的前 项和 =( )A、
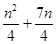 B、
B、 C、
C、 D、
D、 5. 函数 的大致图象为( )A、
5. 函数 的大致图象为( )A、 B、
B、 C、
C、 D、
D、 6. 已知 是定义在R上的偶函数,且在区间 上单调递增.若实数a满足 ,则 的取值范围是( )A、
6. 已知 是定义在R上的偶函数,且在区间 上单调递增.若实数a满足 ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 7. 将函数y=sin x的图像向左平移 个单位,得到函数y=f(x)的图像,则下列说法正确的是( )A、y=f(x)是奇函数 B、y=f(x)的周期为π C、y=f(x)的图像关于直线x=
7. 将函数y=sin x的图像向左平移 个单位,得到函数y=f(x)的图像,则下列说法正确的是( )A、y=f(x)是奇函数 B、y=f(x)的周期为π C、y=f(x)的图像关于直线x=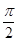 对称
D、y=f(x)的图像关于点
对称
D、y=f(x)的图像关于点  对称
8. 设函数 ,若 的图象与 图象有且仅有两个不同的公共点 ,则下列判断正确的是( )
对称
8. 设函数 ,若 的图象与 图象有且仅有两个不同的公共点 ,则下列判断正确的是( )
A、当 时, B、当 时, C、当 时, D、当 时,9. 已知 , , ,则a, b, c的大小关系为( )A、 B、
B、 C、
C、 D、
D、 10. 设函数f(x)= F(x)=f(x)+x , x∈R.F(x)的值域为( )A、(-∞,1] B、[2,+∞) C、(-∞,1]∪[2,+∞) D、(-∞,1)∪(2,+∞)11. 在 中,角 所对边长分别为 ,若 ,则 的最小值为( )A、 B、
10. 设函数f(x)= F(x)=f(x)+x , x∈R.F(x)的值域为( )A、(-∞,1] B、[2,+∞) C、(-∞,1]∪[2,+∞) D、(-∞,1)∪(2,+∞)11. 在 中,角 所对边长分别为 ,若 ,则 的最小值为( )A、 B、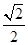 C、
D、
C、
D、 12. 若函数 在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a的取值范围是 ( )A、a≤2 B、5≤a≤7 C、4≤a≤6 D、a≤5或a≥7
12. 若函数 在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a的取值范围是 ( )A、a≤2 B、5≤a≤7 C、4≤a≤6 D、a≤5或a≥7二、填空题
-
13. 设 在约束条件 下,目标函数 的最大值为4,则 的值为 .14. 如图,已知△ABC的外接圆的圆心为O , 两条边上的高的交点为H , 且 ,则实数m=.
 15. 已知函数 在x=-1时有极值0,则 = .16. 设 是等比数列,公比 , 为 的前n项和,记 ',设 为数列 的最大项,则 .
15. 已知函数 在x=-1时有极值0,则 = .16. 设 是等比数列,公比 , 为 的前n项和,记 ',设 为数列 的最大项,则 .三、解答题
-
17. 在△ABC中,p:cosB>0;q:函数y=sin 为减函数.(1)、如果p为假命题,求函数y=sin +B的值域;(2)、若“p且q”为真命题,求B的取值范围.18. 已知各项均不相等的等差数列{an}的前n项和为Sn , 若S3=15,且a3+1为a1+1和a7+1的等比中项.(1)、求数列{an}的通项公式与前n项和Sn;(2)、设Tn为数列{ }的前n项和,问是否存在常数m,使Tn=m[ + ],若存在,求m的值;若不存在,说明理由.19. 的三个内角 对应的三条边长分别是 ,且满足 .
(Ⅰ)求 的值;
(Ⅱ)若 , ,求 和 的值.