陕西省西安市西安理工大学附中2019届九年级上学期数学期中考试试卷
试卷更新日期：2018-12-21 类型：期中考试
一、单选题
-
1. 某反比例函数的图象经过点（-2，3），则此函数图象也经过（ ）A、（2，-3） B、（-3，3） C、（2，3） D、（-4，6）2. 如图，△ABC中，DE∥BC， ，AE=2cm，则AC的长是（ ）
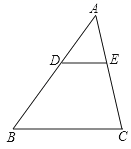A、2cm B、4cm C、6cm D、8cm3. 已知 是关于 的一元二次方程 的一个根，则 的值是（ ）A、1 B、-1 C、0 D、无法确定4. 下面的三视图对应的物体是（ ）
A、
B、
C、
D、
5. 若点（-2， ），（-1， ），（3， ）在双曲线 上，则 ， ， 的大小关系式（ ）A、
< 
< 
B、 < <
C、 < <
D、 < <
6. 已知△ABC~△DEF，S△ABC：S△DEF=9，且△ABC的周长为18，则△DEF的周长为（ ）A、2 B、3 C、6 D、547. 在一个不透明的纸箱中放入m个除颜色外其他都完全相同的球，这些球中有4个红球，每次将球摇匀后任意摸出一个球，记下颜色再放回纸箱中，通过大量重复摸球实验后发现摸到红球的频率稳定在 ，因此可以估算m值是（ ）A、8 B、12 C、16 D、208. 如图，在矩形ABCD中，已知AB=3，AD=8，点E为BC的中点，连接AE，EF是是∠AEC的平分线，交AD于点F，则FD=（ ）
A、3 B、4 C、5 D、69. 如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC= BC．图中相似三角形共有（ ）
A、1对 B、2对 C、3对 D、4对10. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，CH┴AF与点H，那么CH的长是（ ）
A、
B、
C、
D、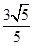
二、填空题
-
11. 方程x2 = 3x的解是.12. 如图，菱形ABCD的面积为6，边AD在x轴上，边BC的中点E在y轴上，反比例函数 的图象经过顶点B，则k的值为 ．
13. 如图，△ABC中，∠C=90º，AC=8，CB=6，在斜边AB上取一点M，是MB=CB，过M作MN┴AB交AC于N，则MN=。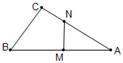
14. 如图，矩形ABCD中，AB=6，MN在边AB上运动，MN=3，AP=2，BQ=5，PM+MN+NQ最小值是。
三、解答题
-
15. 解方程： ．16. 如图，AB、CD、EF是与路灯在同一直线上的三个等高的标杆，已知AB、CD在路灯光下的影长分别为BM、DN，在图中做出EF的影长。
17. 如图，已知O是坐标原点，A、B的坐标分别为（3，1）、（2，-1）.
(1)、在y轴左侧以O为位似中心作△OAB的位似△OCD，要求新图与原图的相似比为2：1；(2)、分别写出A、B的对应点C、D的坐标。18. 若关于x的一元二次方程 有两个相等的实数根，求实数k的值.19. 如图，在Rt△ABC中，∠ACB=90º，点D、E分别是边AB、AC的中点，延长DE至F，使得AF//CD，连接BF、CF。求证：四边形AFCD是菱形。
20. 双塔寺又名水祚寺，是国家级文物保护单位，由于双塔(舍利塔、文峰塔)耸立，被人们称为“文笔双塔”，某校社会实践小组为了测量合利塔的高度，在地面上的C处垂直于地面坚立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，舍利塔的塔尖点B正好在同一直线上，测得EC=4米，将标杆CD向后平移到点G处，这时地面上的点F，标杆的顶端点H，舍利塔的塔尖点B正好在同一直线上(点F，点G，点E，点C与塔底处的点A在同一直线上），这时测得FC =6米，GC =53米，请你根据以上数据，计算舍利塔的高度AB。
21. 某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一.定的关系。每盆植人3株时，平均单株盈利4元；以同样的裁培条件若每盆每增加1株，平均单株盈利就减少0.5元要使每盆的盈利达到14元，且尽可能地减少成本，每盆应该植多少株?22. 如图①，平行四边形OABC的边OC在x轴的正半轴上，OC=5，反比例函数 （x＞0）的图象经过点A（1，4）．
(1)、求反比例函数的关系式和点B的坐标；(2)、如图②，过BC的中点D作DP∥x轴交反比例函数图象于点P，连接AP、OP，求△AOP的面积；23. 小红有青、白、黄、黑四件衬衫，又有米色、蓝色两条裙子，她最喜欢的搭配是白色衬衫配米色裙子，最不喜欢青色衬衫配蓝色裙子或者黑色衬衫配蓝色裙子。(1)、黑暗中，她随机拿出一套衣服正是她最喜欢的搭配的概率是多少?(2)、黑暗中，她随机拿出一套衣服正是她最喜欢的搭配，这样的巧合发生的机会与黑暗中她随机拿出一套衣服正是她最不喜欢的搭配的机会是否相等?画树状图加以分析说明。
